
Es war vor fast 20 Jahren, im lauen Sommer 1996. Ich verdiente gerade mein Geld als Entwickler bei einer bekannten Softwareschmiede im Münchner Osten, als ein Arbeitskollege aufgeregt von einem einfach klingenden aber anscheinend schwer zu lösenden Problem berichtete: Ein befreundeter Rektor sah sich mit der Aufgabe konfrontiert, 9 Lehrer, 27 Schülerinnen und 18 Schüler derart in 9 täglich wechselnde Gruppen einzuteilen, so dass die Schüler an jedem Tag mit anderen Lehrern und Mitschülern in der Klasse sitzen würden. Jede Gruppe bestand aus einem Lehrer, zwei Buben und drei Mädchen, und pro Tag fanden neun Gruppensitzungen in verschiedenen Klassenräumen statt, jeweils geführt von einem der insgesamt neun Lehrer. Wieviele Tage lang könnte man den Unterricht ohne Überlappungen durchziehen? Fünf vielleicht?
Nichts leichter als das! riefen meine Kollegen und ich sofort, legten die Projektarbeit kurzfristig auf Eis und begannen damit, die ersten Programme in unsere Workstations zu klopfen. Abbildung 1 zeigt einen ersten Versuch, mit einem einfachen Algorithmus, der pro Tag neun Gruppen mit immer den gleichen Lehrern und noch nicht eingeteilten Schülern auffüllt. Dabei führt er Buch darüber, wer schon mit wem zusammen war und nimmt für eine Gruppe im Überlappungsfall einfach den nächsten Schüler aus dem noch nicht eingeteilten Kontingent.
Die Lehrer sind mit dem Buchstaben i (für Instructor)
von 1-9 durchnumeriert, die Buben von b1-b18 (Boy) und die Mädchen mit
g1-g27 (Girl). So leitet zum Beispiel Lehrer i1 am ersten Tag in
day1 group1: i1 b1 b2 g1 g2 g3
die Klasse im Gruppenraum 1, mit den Schülern b1 und b2 und den
Schülerinnen g1, g2 und g3.
Am zweiten Tag stellt der Algorithmus in
Gruppe 1 fest, dass die Buben b1 und b2 am Vortag schon mit Lehrer i1 zusammen waren,
und teilt letzterem deswegen b3 und b5 zu. So geht das eine Weile,
allerdings ist schon gegen Ende
des zweiten Schultages Schicht im Schacht, denn für Gruppe 7 finden
sich keine Schülerinnen mehr.
g19, g21 und g21
waren schon am ersten Tag mit i7 in Gruppe 7.
g22, g23 und g24 waren mit
b15 in Gruppe 8. Und
g25, g26 und g27 waren mit b17 in Gruppe 9, also steckt das
Verfahren fest!
Nach einigen Fehlversuchen begann es uns langsam zu dämmern, dass dies wohl etwas mehr Gehirnschmalz und Rechenleistung als zunächst angenommen erfordern würde, also begannen die ersten Informatiker damit, unsere damals brandheißen HPUX-Workstations mit Backtracking-Algorithmen zu traktieren. Zur allgemeinen Überraschung stellte sich jedoch nach einigen Stunden gnadenloser Brute-Force-Attacken kein Erfolg, sondern -- allgemeine Ernüchterung ein. Es gab einfach zuviele Kombinationen, die alle durchzuprobieren vom vornherein zum Scheitern verurteilt war. Keiner der Softwareentwickler im Team, weder die Jungfüchse noch die alten Hasen, hatten auch nur eine Lösung für mehr als zweieinhalb Tage zustande gebracht!
 |
| Abbildung 1: Wer die Gruppen der Reihe nach mit Schülern auffüllt, schafft nicht mal zwei Tage ohne Überlappungen. |
Wo Hilfe suchen? Das Internet steckte 1996 noch in den Kinderschuhen, das Web war völlig unbrauchbar, weil es hauptsächlich aus "Homepages" bestand, die aufgeregt mit BLINK-Tags und den schaufelnden Bauarbeitern des "Under Construction"-Zeichens warben. Google kam erst zwei Jahre später, also hätte ich etwaige Lösungen, selbst wenn es sie gegeben hätte, in Bergen von Spamseiten nie gefunden. Aber das Usenet gab es schon und wurde hauptsächlich von Universitätsangestellten frequentiert, also so ich machte mich daran, das Problem auf der Newsgroup rec.puzzles zu schildern und die Gemeinde dort um Hilfe zu bitten ([2] und Abbildung 2).
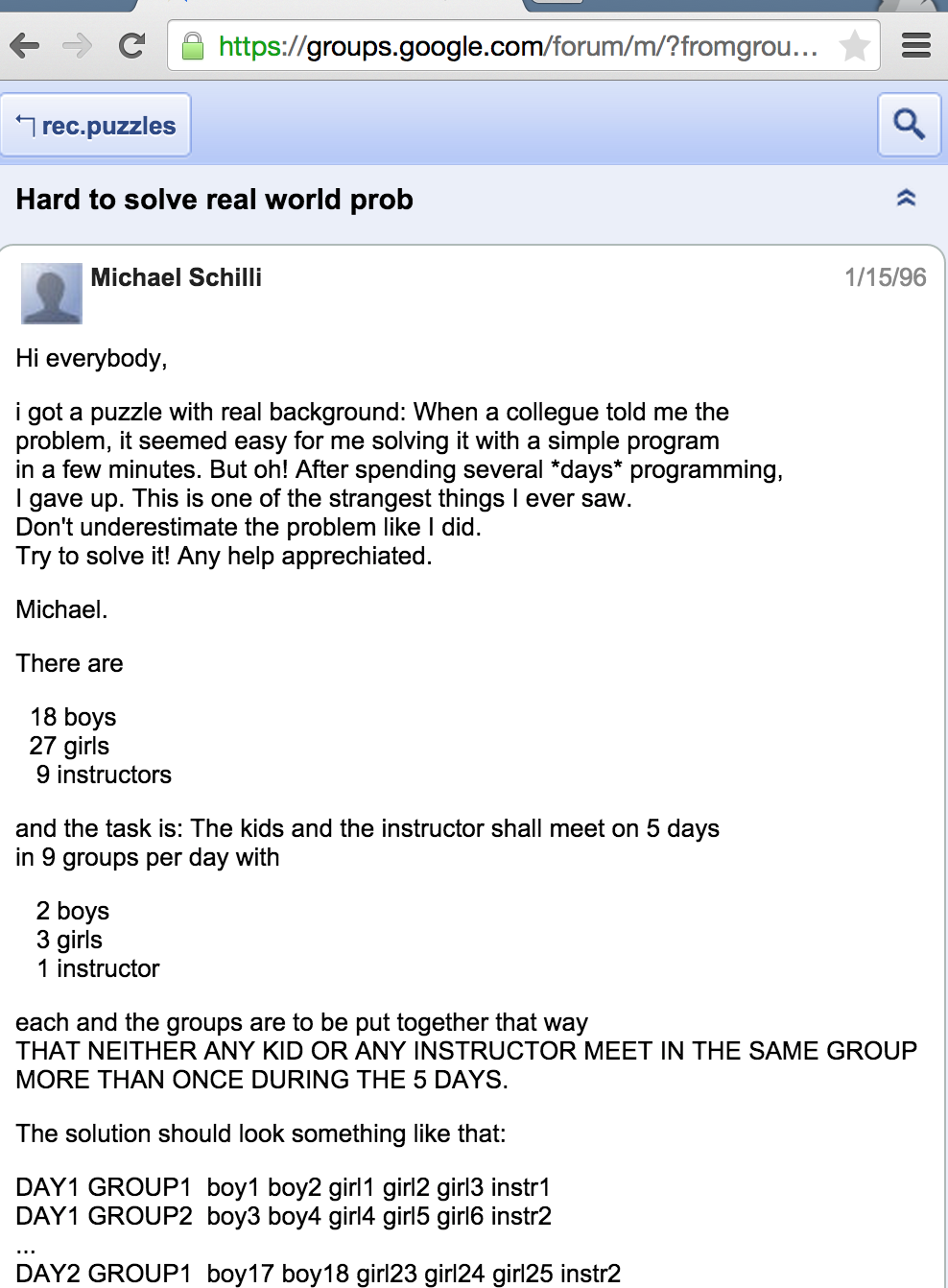 |
| Abbildung 2: Der Usenet-Artikel von 1996 mit dem alles anfing. |
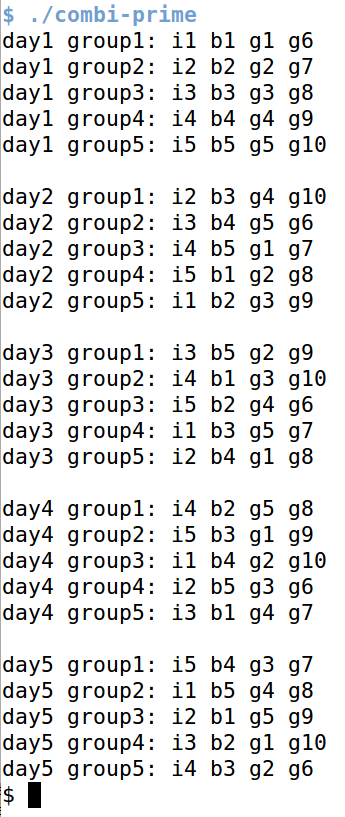
Ein paar Tage später kam die Antwort eines Mathematikers namens Barry Wolk von der Universität Manitoba in Kanada. Er hatte das Problem mit schweren Geschützen diskreter Mathematik gelöst: einem Galoiskörper mit neun Elementen und neun daraus generierten zueinander orthogonalen Lateinischen Quadraten ("Latin Squares", [3], [4]). Ich fabrizierte aus seinen glasklaren und selbst für mathematische Laien verständlichen Instruktionen schnell ein Perlskript, das im Bruchteil einer Sekunden eine Lösung für nicht nur fünf, sondern ganze neun Tage ausspuckte (Abbildung 3). Ich war der Held!
 |
| Abbildung 3: In Sekundenschnelle druckt der diskret-mathematische Ansatz eine Lösung für insgesamt neun Tage aus. |
Was der kanadische Mathematiker vorschlug, war, eine Sammlung von sogenannten "Lateinischen Quadraten" zu konstruieren. Diese matrixförmigen, and Soduko-Rätsel erinnernden Gebilde, an denen schon der kauzige Österreicher Leonhard Euler im 18. Jahrhundert seine Freude fand, enthalten die Zahlen von 1-N pro Spalte oder Reihe genau einmal. Abbildung 4 zeigt ein lateinisches Quadrat der Dimension 9x9 mit den Zahlen 1-9. Wer durch die Spalten und Reihen fährt, kann leicht feststellen, dass sich keine einzige Zahl weder auf der Senkrechten noch auf der Waagrechten jemals wiederholt. Euler füllte seine Quadrate damals übrigens statt mit Zahlen mit lateinischen Großbuchstaben A, B, ..., und deswegen kam der "lateinische" Namenszusatz zustande.
 |
| Abbildung 4: Ein Lateinisches Quadrat der Größe 9x9. |
Zum Zusammenwürfeln von Schülern zu Gruppen an mehreren Tagen fehlt bei den Quadraten allerdings noch eine weitere Dimension: Hierzu benötigt man insgesamt N-1 dieser Lateinischen Quadrate, die zueinander orthogonal sind, was heißt, dass wenn man ein Monsterquadrat aus der Überlagerung der x-y-Werte aller Quadrate erzeugt, die erzeugten Kombinationen alle eindeutig sind.
Abbildung 5 zeigt zum Beispiel vier zueinander orthogonale Lateinische Quadrate ("Mutually Orthogonal Latin Squares" oder "MOLS") der Dimension 5x5. Von Bedeutung sind momentan nur die blau eingezeichneten Werte, die schwarzen Werte am Rand kommen später zum Zug. Alle vier Quadrate elementweise zusammengefasst ergeben das Megaquadrat in Abbildung 6, dessen Einträge jeweils aus den entsprechenden Werten der drei Originalquadrate an der gleichen Position bestehen. In den Originalen stehen zum Beispiel in der 4. Reihe der 1. Spalte die Werte 5, 4, 3 und 2, weshalb im überlagerten Quadrat an derselben Stelle der Wert "5432" steht.
 |
| Abbildung 5: Da 5 eine Primzahl ist, sind vier zueinander orthogonale lateinische Quadrate (MOLS) schnell generiert. |
 |
| Abbildung 6: Die vier MOLS aus Abbildung 5 zusammengefasst ergeben lauter eindeutige Kombinationen. |
Aus diesem Megaquadrat lassen sich nun die gesuchten Gruppen sehr einfach so zusammenstellen, dass es an mehreren aufeinander folgenden Tagen zwischen den Teilnehmern zu keinerlei Überlappungen kommt. Da es sich nur um 5x5-Quadrate und handelt, kann das Verfahren nur fünf Tage lang jeweils fünf Gruppen mit jeweils vier (N-1) Teilnehmern erzeugen, also zum Beispiel einem Lehrer (von insgesamt fünfen), einem Schüler (von ebenfalls fünfen) und zwei Schülerinnen (von insgesamt 10). Abbildung 7 zeigt das Ergebnis, das praktisch nur eine simple Transformation der Einträge des Megaquadrates in Abbildung 6 ist. Das Skript in Listing 1 wandert von links nach rechts und von oben nach unten durch die Einträge und münzt sie auf die Personen um. Der Eintrag "1111" wird so zu "i1 b1 g1 g6", denn es handelt sich um den ersten Lehrer, den ersten Buben, die erste Schülerin aus der ersten Gruppe und die erste Schülerin aus der zweiten Gruppe. Der Eintrag "3524" wird entsprechend zu "i3 b5 g2 g9", und so weiter.
 |
| Abbildung 7: Gruppen aus je einem Lehrer, einem Schüler und zwei Schülerinnen aus vier 5x5 MOLS. |
Wie aber erzeugt das Skript anfangs die vier zueinander orthogonalen lateinischen Quadrate, aus denen sich dann mühelos die Gruppeneinteilung ableiten lässt? Da es sich um Quadrate der Dimension 5x5 handelt und 5 eine Primzahl ist, ist das Verfahren ganz einfach.
01 #!/usr/bin/perl -w
02 use strict;
03
04 my @lineup = qw( 0 2 3 4 1 );
05 my $size = scalar @lineup;
06 my @as = qw( 1 2 3 4 );
07 my @squares = ();
08
09 for my $aidx ( 0..$#as ) {
10 for my $ridx ( 0..$#lineup ) {
11 for my $cidx ( 0..$#lineup ) {
12 my $row = $lineup[ $ridx ];
13 my $col = $lineup[ $cidx ];
14 my $a = $as[ $aidx ];
15 my $v = ( $a * $row + $col ) % $size;
16 $squares[ $aidx ]->[ $ridx ]->[ $cidx ]
17 = $v + 1;
18 }
19 }
20 }
21
22 for my $day ( 1..$size ) {
23 for my $group ( 1..$size ) {
24 my @v = ();
25 for my $sidx ( 0..$size-2 ) {
26 push @v, $squares[ $sidx ]->
27 [ $day - 1]->[ $group - 1 ];
28 }
29
30 my( $i, $b, $g1, $g2 ) = @v;
31 $g2 = $g2 + $size;
32 print "day$day group$group:",
33 " i$i b$b g$g1 g$g2\n";
34 }
35 print "\n";
36 }
In Abbildung 5 stehen am Rand der Quadrate jeweils in Schwarz die x- und
y-Werte von 0 bis 4 in durchgewürfelter Reihenfolge,
da diese keine Rolle spielt. Jedes Element der Matrix berechnet sich
nun nach der einfachen Formel (a*y + x) % 5 + 1, wobei a beim ersten
Quadrat auf 1 gesetzt wird, beim zweiten auf 2, und so weiter.
So ergibt sich zum Beispiel
für das Element in der zweiten Spalte der dritten Reihe
des vierten Quadrats liegt, folgender Wert: Da der y-Wert
der 3. Reihe des vierten Quadrats auf 3
steht, der x-Wert der zweiten Spalte auf 2, und der Wert für a im
vierten Quadrat 4 beträgt, ergibt sich 4 * 3 + 2 = 14.
Auf modulo 5 reduziert bleiben 4 übrig, und 1 dazugezählt, weil die
Werte von 1-5 laufen und nicht von 0-4, macht 5.
Listing 1 implementiert diese Formel einfach in den beiden for-Schleifen
ab Zeile 9 und macht sich dann im abschließenden Teil ab Zeile 22 daran,
die Kombinationen auszugeben. Das Ganze läuft rasend schnell, da es sich
um simple Arithmetik und kein Probierverfahren handelt.
Aber natürlich gilt "Vertrauen ist gut, Kontrolle ist besser" und Listing
2 liest die formatierte
Ausgabe von Listing 1, und prüft mittels der Hashreferenz
$met ob die Teilnehmer tatsächlich jedes Mal mit anderen Leuten
zusammensitzen. Kehrt das Skript ohne Ausgabe zurück, stimmt alles.
01 #!/usr/bin/perl -w
02 use strict;
03
04 my $met = {};
05
06 while( <> ) {
07 # day9 group1: i9 b9 b18 g9 g18 g27
08 if( my( $day, $group, $rest ) =
09 /day(\d+)\s
10 group(\d+):\s
11 (.*)
12 /x ) {
13 my @participants = split / /, $rest;
14
15 for my $i ( 0 .. $#participants ) {
16 for my $j (
17 $i+1 .. $#participants ) {
18 my $a = $participants[ $i ];
19 my $b = $participants[ $j ];
20
21 if( exists $met->{ $a }->{ $b } or
22 exists $met->{ $b }->{ $a } ) {
23 die "$day:$group: Whoops, $a ",
24 "and $b have met already ",
25 "on $met->{ $a }->{ $b }";
26 }
27
28 $met->{ $a }->{ $b } =
29 $met->{ $b }->{ $a } =
30 "$day:$group";
31 }
32 }
33 }
34 }
Ist die Felddimension allerdings keine Primzahl, wie bei den eingangs geforderten Quadraten der Größe 9x9, wird die Sache schon schwieriger. Für eine Anordnung der Dimension 6x6 hingegen gibt es überhaupt keine Lösung, was Euler herausfand als er 36 Offiziere aus 6 verschiedenen Regimenten mit jeweils 6 unterschiedlichen Diensträngen so für eine Parade aufmarschieren lassen wollte, dass sich weder Dienstränge noch Regimentszugehörigkeit innerhalb einer Reihe oder Rotte wiederholten ([6]). Er schloss richtigerweise, dass das theoretisch unmöglich sei, ließ sich aber auch gleich leichtsinnigerweise und voreilig zu der Vermutung hinreißen, dass es für Dimensionen 4n+2 generell keine Lösung gäbe. Riesenfehler! Mehr als 150 Jahre später, 1959, stellte sich heraus, dass es auch Lösungen für 10x10 und sogar 14x14 gibt. Dass das Problem der 36 Offiziere aber garantiert unlösbar ist, das wurde mittlerweile ebenfalls wasserdicht bewiesen.
Ist die Dimension allerdings eine Primzahlpotenz (also zum Beispiel 9, was die zweite Potenz der Primzahl 3 ist), dann bedient sich der Fachmann bei Konstruktion der Quadrate eines sogenannten Galoiskörpers F. Dies ist eine Ansammlung von N Zahlen, auf die die Rechenoperationen Addition (+) und Multiplikation (*) definiert sind, die wiederum ein Ergebnis in F liefern.
Bezogen auf das Problem mit den 9 Lehrern, 18 Schülern und 27 Schülerinnen schlug der kanadische Mathematiker vor, diese in insgesamt 6 Gruppen mit je 9 Teilnehmern einzuteilen: die Lehrer, die A- und die B-Schüler, und die C-, D- und E-Schülerinnen. Diesen rückte er dann mit dem neun-elementigen aus komplexen Zahlen (i^2 = -1) bestehenden Körper
F = { 0, 1, 2, i, 1+i, 2+i,
2i, 1+2i, 2+2i }
zuleibe, der Addition und Multiplikation mittels Modulo 3 reduziert und damit sicherstellt, dass eine Verknüpfung zweier Elemente aus F wieder ein Element aus F zum Ergebnis hat. So liefert zum Beispiel
(1 + 2i) * (1 + i) = -1 + 3i
was sich Modulo 3 zu 2 + 0i also 2 reduzieren lässt, was
wiederum in F liegt. Wenn wir mit + und * die an den Körper
angepassten Operationen Modulo 3 bezeichnen, lassen sich die
Nummern der Teilnehmer in den Gruppen mit
den Formeln in Abbildung 8 die Quadrate erzeugen. Die Variable
d bezeichnet dabei jeweils die Nummer des Tages (1 bis 9) und
g die Nummer der Gruppe (ebenfalls 1 bis 9), heraus kommt jeweils
die Nummer des Teilnehmers aus den 6 verschiedenen Teilklassen, der
zum angegebenen Tag in der jeweiligen Gruppe sitzt.
 |
| Abbildung 8: Diese Formeln bestimmen, welcher Lehrer und welche Schüler am Tag d in Gruppe g sitzen. |
01 #!/usr/local/bin/perl -w
02 use strict;
03 use warnings;
04
05 my @field = (
06 [ 0, 0 ], [ 1, 0 ], [ 2, 0 ],
07 [ 0, 1 ], [ 1, 1 ], [ 2, 1 ],
08 [ 0, 2 ], [ 1, 2 ], [ 2, 2 ],
09 );
10
11 # map re/im => field element number
12 my $lookup = { };
13 for my $idx (1 .. scalar @field ) {
14 my( $re, $im ) = @{ $field[ $idx - 1 ] };
15 $lookup->{ $re }->{ $im } = $idx;
16 }
17 sub mapback {
18 my( $re, $im ) = @_;
19 return $lookup->{ $re }->{ $im };
20 }
21
22 foreach my $day (1..9) {
23 foreach my $group (1..9) {
24 print "day$day group$group: ";
25 print "i", fadd( $day,
26 fmult( 2, $group ) ), " ";
27 print "b", fadd( $day,
28 fmult( 3, $group ) ), " ";
29 print "b", fadd( $day,
30 fmult( 4, $group ) ) + 9, " ";
31 print "g", fadd( $day,
32 fmult( 5, $group ) ), " ";
33 print "g", fadd( $day,
34 fmult( 6, $group ) ) + 9, " ";
35 print "g", fadd( $day,
36 fmult( 7, $group ) ) + 18, "\n";
37 }
38 print "\n";
39 }
40
41 sub fadd {
42 my( $f1, $f2 ) = @_;
43
44 my( $r1, $i1 ) = @{ $field[ $f1 - 1 ] };
45 my( $r2, $i2 ) = @{ $field[ $f2 - 1 ] };
46
47 return mapback(
48 ( $r1 + $r2 ) % 3,
49 ( $i1 + $i2 ) % 3 );
50 }
51
52 sub fmult {
53 my( $f1, $f2 ) = @_;
54
55 my( $r1, $i1 ) = @{ $field[ $f1 - 1 ] };
56 my( $r2, $i2 ) = @{ $field[ $f2 - 1 ] };
57
58 return mapback(
59 ( $r1 * $r2 - $i1 * $i2 ) % 3,
60 ( $r1 * $i2 + $r2 * $i1 ) % 3 );
61 }
Listing 3 implementiert diese Formeln lediglich und spuckt das Ergebnis
für neun Tage wie eingangs in Abbildung 3 gezeigt aus. Die komplexen
Zahlen im Galoiskörper definiert dabei das Array @field in Zeile 5,
und die ab Zeile 17 stehende Funktion mapback sucht zu einer Zahl
(zum Beispiel dem Ergebnis einer Multiplikation) wieder die Nummer
des Elements in F heraus. Die Funktionen fadd() und fmult()
(Zeile 41 bzw. 52) implementieren die per Modulo 3 reduzierte
Addition bzw. Multiplikation zweier Feldelemente aus F. Sie nehmen
die Feldnummern der Elemente entgegen, suchen die zugehörigen komplexen
Zahlen aus F heraus, führen die jeweilige Operation auf den Real-
und den Imaginärteil der Operanden durch, und führen das Ergebnis wieder
mit mapback auf die Nummer eines Elements aus F zurück.
Der Galoiskörper ist nach dem französischen Mathematiker Évariste Galois benannt, der den wesentlichen Durchbruch schon im zarten Alter von 18 Jahren errang. Was er noch alles erreichen hätte können, bleibt Spekulation, denn mit 20 ließ er sich zu einem Pistolenduell hinreißen, bei dem er den Kürzeren zog und am Tag darauf seiner Schussverletzung erlag. So ging's zu im 19. Jahrhundert, heute Meilensteine der diskreten Mathematik legen, und morgen früh mit der Steinschlosspistole in der Hand raustreten, um Beleidiger umzunieten, damals war noch was geboten!
Listings zu diesem Artikel: ftp://www.linux-magazin.de/pub/listings/magazin/2015/08/Perl
Usenet-Posting aus dem Jahr 1996: https://groups.google.com/forum/m/?fromgroups#!topic/rec.puzzles/kSsEDkm1_gw
"Galoiskörper", Wikipedia-Eintrag http://de.wikipedia.org/wiki/Endlicher_K%C3%B6rper
"Lateinisches Quadrat", Wikipedia-Eintrag http://de.wikipedia.org/wiki/Lateinisches_Quadrat
"Mutually Orthogonal Latin Squares and Finite Fields", Padraic Bartlett, 2012 http://math.ucsb.edu/~padraic/mathcamp_2012/latin_squares/MC2012_LatinSquares_lecture2.pdf
"Thirty-six officers problem", http://en.wikipedia.org/wiki/Thirty-six_officers_problem