Neuronale Netzwerke leisten bereits Großartiges, wenn es darum geht, verrauschte Muster in Eingangsdaten zu erkennen und sie eindeutigen Ergebnissen zuzuordnen. Wenn ein Dutzend Personen die Buchstaben "A" oder "B" in unterschiedlichen Handschriften in ein Formular eintragen, fieselt ein trainiertes Netzwerk aus dem Abzug problemlos jedesmal das richtige Ergebnis heraus. Und eine Mustererkennung für Nummernschilder vorbeizischender Fahrzeuge extrahiert auf den Fotos zielsicher die Autokennzeichen und liest die darauf stehenden Buchstaben, damit der Verkehrsminister auch genau weiß, wer wann wohin gefahren ist.
Hat ein neuronales Netzwerk aber einmal ausgelernt, ordnet es den gleichen Eingangsdaten immer das gleiche Ergebnis zu. Bei Aufgaben, die sich darum drehen, aus zeitdiskreten Wertefolgen den folgenden Wert ermitteln, schneiden sie oft nicht optimal ab, besonders falls das Eingangssignal Schwankungen unbekannter Periodizität unterliegt.
In neuronalen Netzwerken justiert der Lernalgorithmus interne Gewichte anhand der Trainingsdaten, die sich dann aber zur Laufzeit nicht mehr ändern, also keine temporalen Änderungen in den Eingangsdaten berücksichtigen können, da der Automat sich keinen Zustand merkt. Zwar führen in sogenannten Recurrent Neural Networks (RNN) interne Verbindungen wieder zurück zum Eingang und beeinflussen so den nächsten Eingabevektor, doch reicht das bei simplen Netzwerken nicht aus, um zeitliche Muster zu erkennen, die sich über mehrere Zyklen erstrecken.
| |
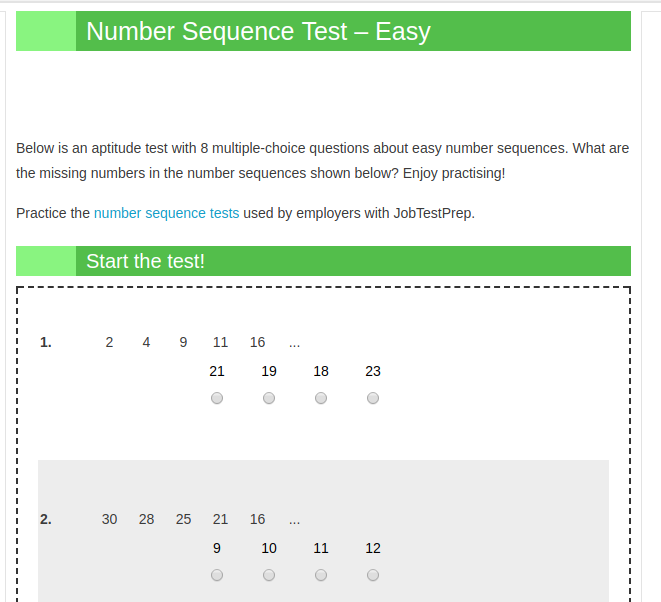
| Abbildung 1: Ein Intelligenztest, bei dem der Kandidat eine Ziffernfolge ergänzen muss ([2]). |
Ein amüsantes Beispiel zum Vorhersagen von Sequenzen sind die bei manchen Psychologen beliebten Intelligenztests, bei denen der Kandidat anhand einer Ziffernfolge ermitteln muss, welche Ziffer wohl als nächstes kommt. Ein Kind im Schulalter kann wohl sagen, dass nach 2, 4, 6 als nächstes "8" kommt, aber wie sieht es mit der Folge 2, 5, 7, 10, 12 aus?
 |
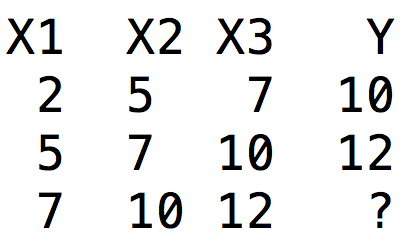| Abbildung 2: Ein- und Ausgabewerte zum Trainieren des LSTM-Netzwerks. |
Abbildung 2 zeigt zwei Lernschritte und einen Testschritt für ein "Long
Short-Term Memory"-(LSTM)-Netzwerk, das lernen soll, welche Zahl wohl nach
der 12 in der obigen Sequenz kommt. Im ersten Lernschritt in der ersten Reihe
der Matrix erfährt es, dass auf die Kombination 2,5,7 immer eine 10
folgt. Die zweite Reihe weist der um eins verschobenen Teilfolge 5,7,10 als
Ergebnis die "12" zu. Mit diesen Trainingsdaten justiert das LSTM-Netzwerk die
Parameter seiner internen Zellen (Abbildung 3). Anders als bei einem
klassischen neuronalen Netzwerk produziert nicht jeder Eingabewert sogleich
einen Ausgabewert, sondern es merkt sich den aktuellen Zustand in einer
Speicherzelle (Abbildung 4), um erst nach der (im vorliegenden Fall) dritten
Eingabe und unter Auswertung des bis dahin auf jedem Zeitschritt
mitgeschleppten Zustands einen Ausgabewert (y(1)) zu produzieren.
 |
| Abbildung 3: Long Short-Term Memory-Zelle. |
Link Wikipedia: https://upload.wikimedia.org/wikipedia/commons/5/53/Peephole_Long_Short-Term_Memory.svg
 |
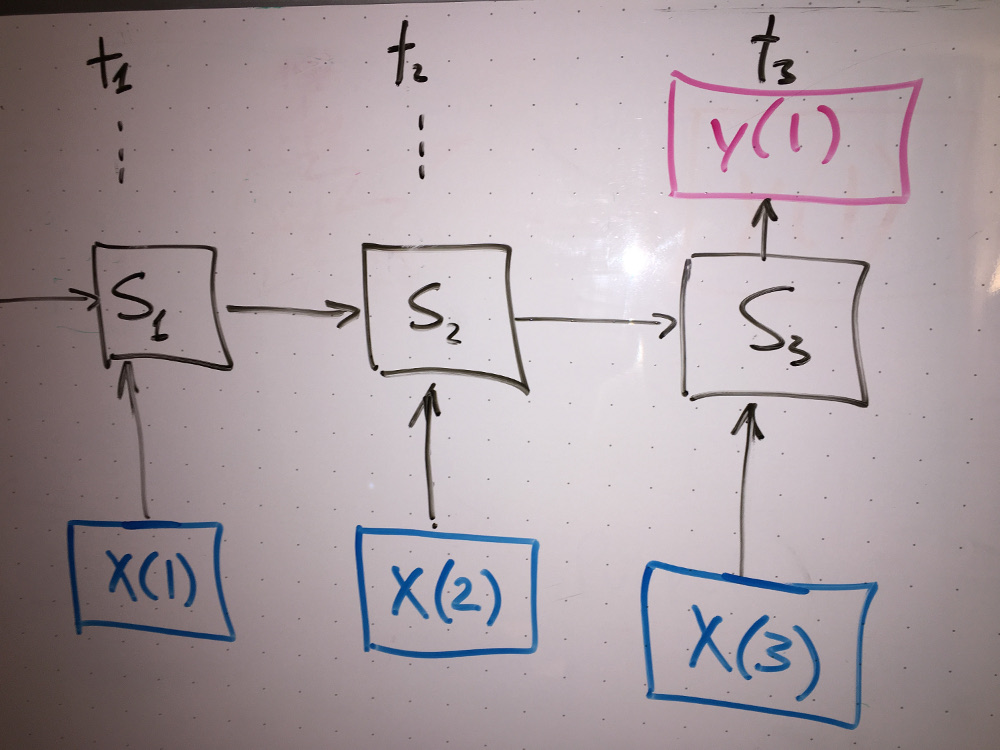| Abbildung 4: Zeitlich auf einander folgende Eingabewerte verändern im Modell zunächst nur den aktuellen Status und produzieren erst alle drei Zeitschritte einen Ausgabewert. |
Zur Implementierung des LSTM-Netzwerks greift das Skript in Listing 1 auf
die Python-Library Keras zu.
Da viele ihrer Funktionen Daten in Form von Matrizen entgegennehmen, bietet
sich vor dem eigentlichen Arbeitsgang eine kurze Erläuterung der Funktion
reshape() aus der Numpy-Array-Library an, um die Matrizen ordnungsgemäß
aufzubrezeln.
 |
| Abbildung 5: Ein Numpy-Array nimmt mit reshape() verschiedene Dimensionen an. |
Einen eindimensionalen Numpy-Array (also einen Vektor) wandelt die
Methode reshape() wie in Abbildung 5 gezeigt flugs in Matrizen
voreingestellter Dimensionen um. Dabei gibt der erste Parameter an
reshape() die Anzahl der Elemente der ersten Dimension an, gefolgt
von der Anzahl der zweiten, dritten und so weiter. Da die Anzahl der
Elemente in der ersten Dimension implizit feststeht, nachdem tiefere
Dimensionen festgelegt wurden, wird erstere oft als -1 angegeben,
dann tut die Library das Richtige und füllt die Matrix mit den übrigen
Elementen auf. Mit nur einem Parameter aufgerufen (reshape(-1)), macht
die Methode aus einer beliebig verschachtelten Array-Struktur wieder einen
eindimensionalen Vektor.
Mit einem Array wie [3,4,5,6,7] aufgerufen (Abbildung 6) produziert das
Skript relativ genau die auf die Sequenz folgende Zahl (7.84 statt 8).
Listing 1 zerlegt dazu
die Zahlenreihe mittels der ab Zeile 11 definierten Funktion window
in wandernde 4er-Blöcke ([3,4,5,6], [4,5,6,7]) und legt jeweils die ersten
drei Elemente im Eingabevektor X
und das letzte Element im Ergebnisvektor y ab.
 |
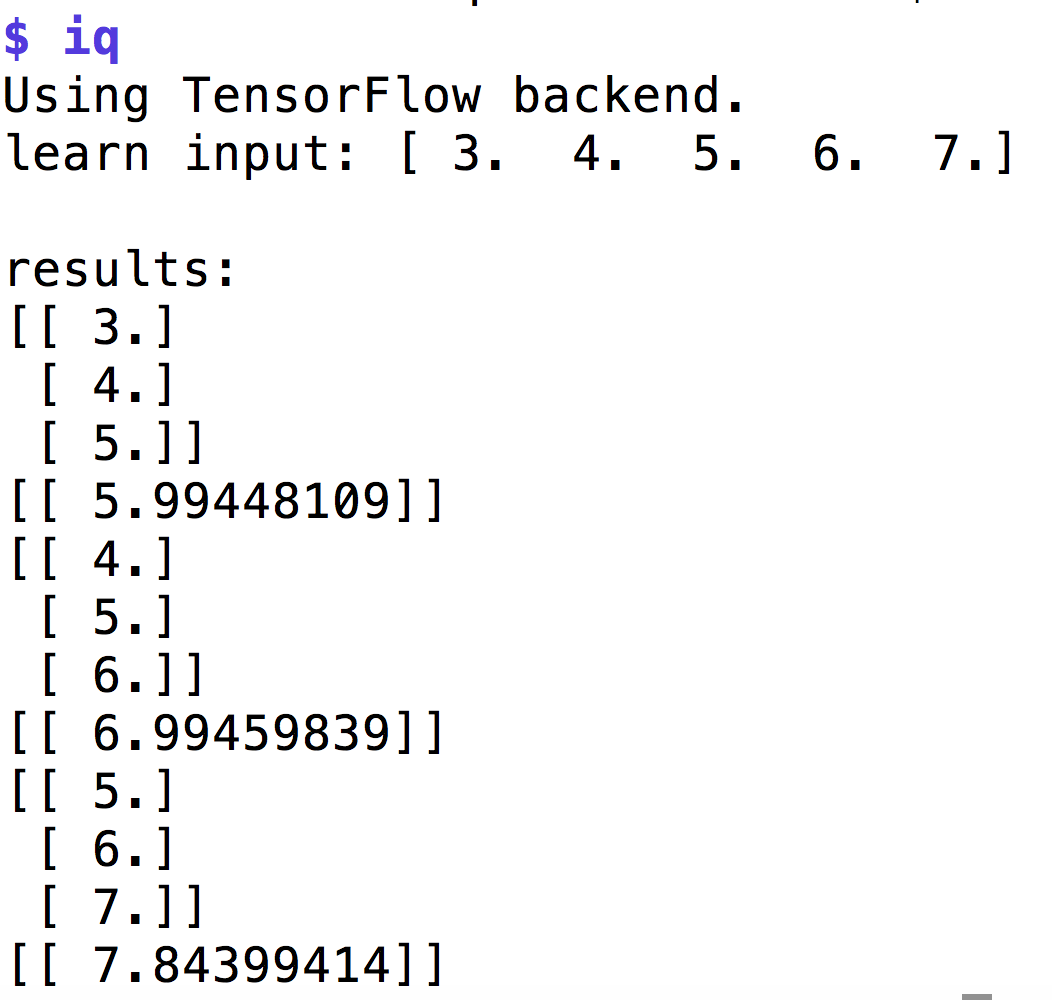| Abbildung 6: Eine einfache Sequenz packt das LSTM-Netzwerk relativ zielsicher. |
Damit dem LSTM-Netzwerk nicht gleich seine Gewichte um die Ohren fliegen,
normalisiert der aus der sklearn-Library stammende StandardScaler
die Werte noch auf kleine sowohl positive als auch negative
Floatingpointzahlen um den Nullpunkt herum, sowohl für den Eingabe- aus
auch den Ergebnisvektor, der die zum Supervised Learning notwendigen
erwarteten richtigen Ergebnisse enthält. Die Methode fit_transform()
standartisiert die Daten, weiter unten, wenn es an die Ausgabe der
Ergebnisse geht, dreht inverse_transform() den Spieß wieder um und
holt zur erbaulichen Betrachtung die Originaldaten wieder hervor.
01 #!/usr/bin/python3
02 import numpy as np
03 from sklearn.preprocessing \
04 import StandardScaler
05 from keras.models import Sequential
06 from keras.layers import Dense, Activation
07 from keras.layers import LSTM
08 import os
09
10 os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
11
12 def window(npa, n=2):
13 for start in range(npa.size-n+1):
14 yield npa[start:start+n:1]
15
16 input_size=3
17
18 seq= np.array(
19 [2,5,7,10,12]).astype('float64')
20
21 print("learn input: " + str(seq))
22
23 scaler = StandardScaler()
24 seq = seq.reshape(-1,1)
25 seq = scaler.fit_transform(seq)
26 seq = seq.reshape(-1)
27
28 X=np.array([])
29 y=np.array([])
30
31 for chunk in window(seq, n=input_size+1):
32 X=np.append(X, chunk[:-1])
33 y=np.append(y, chunk[-1])
34
35 X=X.reshape((-1,input_size,1))
36 y=y.reshape((-1,1))
37
38 model = Sequential()
39 model.add(LSTM(5,
40 input_shape=(input_size,1)))
41 model.add(Dense(1))
42 model.add(Activation("linear"))
43 model.compile(loss="mean_squared_error",
44 optimizer="rmsprop")
45 model.fit(X,y, epochs=500, verbose=0)
46
47 print("\nresults:")
48 for input in X:
49 input=input.reshape(1,input_size,1)
50 pred=model.predict(input)
51 print(scaler.inverse_transform(
52 input.reshape(-1,1)))
53 print(scaler.inverse_transform(
54 pred.reshape(-1,1)))
55
56 test = seq[-input_size::1]
57 print(scaler.inverse_transform(
58 test.reshape(-1,1)))
59 test=test.reshape(1,input_size,1)
60 y1=model.predict(test)
61 print(scaler.inverse_transform(
62 y1.reshape(-1,1)))
Die Zeilen 38 bis 45 stapeln die verschiedenen Layer des LSTM-Netzwerks
aufeinander. Als erstes kommt in Zeile 39 der LSTM-Core-Layer mit 5 internen
Neuronen hinzu. Es folgt der Ausgabe-Layer unter dem Namen Dense und
die Activation-Funktion, die die Antwortkurve der intern verwendeten Neuronen
auf "linear" setzt, da dies beim Testen die besten Ergebnisse brachte.
Anschließend macht compile() das Lernmodell startfertig und bestimmt
außerdem als Lernparameter "mean_squared_error" (Abweichungen vom
optimalen Lernerfolg werden nach der Methode der mittleren Quadrate gemessen)
und als Optimizer den Algorithmus "rmsprop", ein bei neuronalen Netzwerken
gängiges Verfahren.
Zeile 45 ruft nun die Methode fit() des Modells auf, übergibt ihr
die Lerndaten und verlangt mit epoch=500 entsprechend viele
Lerndurchgänge. Im Test zeigte sich bei kürzeren Lernphasen schlechtere
Ergebnisse, doch größere Werte für epoch halfen nicht nach dem Motto
"viel hilft viel" zu mehr Lernerfolg, da sich das System danach
auspendelte und der Lernprozess (sichtbar am gleichbleibenden Wert
für die "loss"-Funktion) stagnierte.
 |
| Abbildung 7: Bei einer zyklischen Sequenz sagt der Algorithmus den jeweils nächsten Wert ungefähr richtig voraus. |
Der letzte Abschnitt von Listing 1 ab Zeile 47 gibt dann nur noch die mit dem austrainierten Modell erzielten Vorhersagen aus, sowohl für die Trainingsdaten als auch für die Fortsetzung der Folge, die das System rein aus vorher Gelerntem ableiten muss, da sich in den Trainingsdaten kein entprechender Präzedenzfall findet.
Abbildung 7 zeigt, dass das Netzwerk auch bei zyklischen Daten (1,2,3,1,2,3) eine gute Figur macht, übrigens unabhängig davon, wie lang die Periode des Signals ist. Das ist ein wesentlicher Vorteil gegenüber klassischen neuronalen Netzwerken, denen man die Periodizität vorher zustecken muss, damit sie zuverlässige Vorhersagen machen.
 |
| Abbildung 8: Beim Intelligenztest schneidet das LSTM-Netzwerk nicht gut ab, da es versucht, da es die unterschiedlichen Zuwachsraten nicht erkennt. |
Um die keras-Library zu auf den heimischen Rechner zu holen,
sind folgende Bibliotheken
aus dem Python-Fundus zu installieren:
$ pip3 install --user keras pandas tensorflow sklearn numpy
$ sudo apt-get install python-tk
Gerade der von keras verwendete Tensorflow-Backend ist nicht gerade
ein Geschwindigkeitsmonster, auf meinem etwa 5 Jahre alten PC dauerte
es gute 10 Sekunden, bis das Programm überhaupt erst mal loslegte.
Beim Intelligenztest machte das Netzwerk allerdings keine so gute Figur.
Der Trick bei der Serie 2,5,7,10,12 ist, wie die Ratefüchse unter
den Lesern sicher sogleich erkannt haben, abwechselnd 3 und 2 zu den
Zahlen hinzuzuaddieren, um auf die nächste Zahl der Folge zu kommen.
Da der letzte Sprung von 10 auf 12 nur zwei Einheiten lang war, muss die
nächste Zahl wieder 3 Werte weiter vorne liegen, also ist 15 das erwartete
Ergebnis für unsere Leser mit ihren erstaunlich hohen Intelligenzquotienten.
Das Netzwerk tendierte aber eher zu 14, konnte also mit menschlicher
Intelligenz (noch) nicht ganz mithalten.
Listings zu diesem Artikel: http://www.linux-magazin.de/static/listings/magazin/2017/10/snapshot/
"Number Sequence Test", https://www.fibonicci.com/numerical-reasoning/number-sequences-test/easy/
"Long Short-Term Memory Networks with Python", Jason Brownlee, Machine Learning Mastery, 2017, https://machinelearningmastery.com/lstms-with-python/
 |
Michael Schilliarbeitet als Software-Engineer in der San Francisco Bay Area in Kalifornien. In seiner seit 1997 laufenden Kolumne forscht er jeden Monat nach praktischen Anwendungen verschiedener Programmiersprachen. Unter mschilli@perlmeister.com beantwortet er gerne Ihre Fragen. |