Glaubt man Wikipedia [2], scheinen Labyrinthe schon ägyptische Pharaonen und die alten Griechen fasziniert zu haben, vermuten zumindest einige Archäologen. In Europa kamen Irrgärten ab dem 15. Jahrhundert in Mode, meist auf herrschaftlichen Gütern, auf denen sich Gäste in mittels hoher Hecken unterteilten Gartenanlagen lustwandelnd verirren durften.
Verschlungene Pfade, die teilweise sogar im Kreis führen, und auf denen es gilt, von einem Startpunkt aus zu einem Endpunkt zu gelangen, lassen sich aber auch auf Papier zeichnen oder im Computer simulieren. Programme stellen das Wegesystem intern meist als Graphen dar, auf dessen Kanten der virtuelle Gast sich von einem Knoten zum nächsten hangelt, Sackgassen verwirft, aus Endlosschleifen aussteigt, und irgendwann am Zielknoten ankommt.
Die computergestützte Behandlung von Labyrinthen teilt sich in zwei Aufgaben: Einmal die Erzeugung von Irrgärten und zweitens deren möglichst effektive Durchschreitung mittels eines Lösungsprogramms (Solver). Man sollte es nicht für möglich halten, aber auf Amazon hat tatsächlich jemand ein Buch zum Thema "Labyrinthe für Programmierer" eingestellt ([3]). Dessen Kindle-Version ist zwar wegen Fontproblemen gründlich misslungen, aber die Papierausgabe zeigt einige nützliche Verfahren zum Erstellen und Lösen von Labyrinthen.
 |
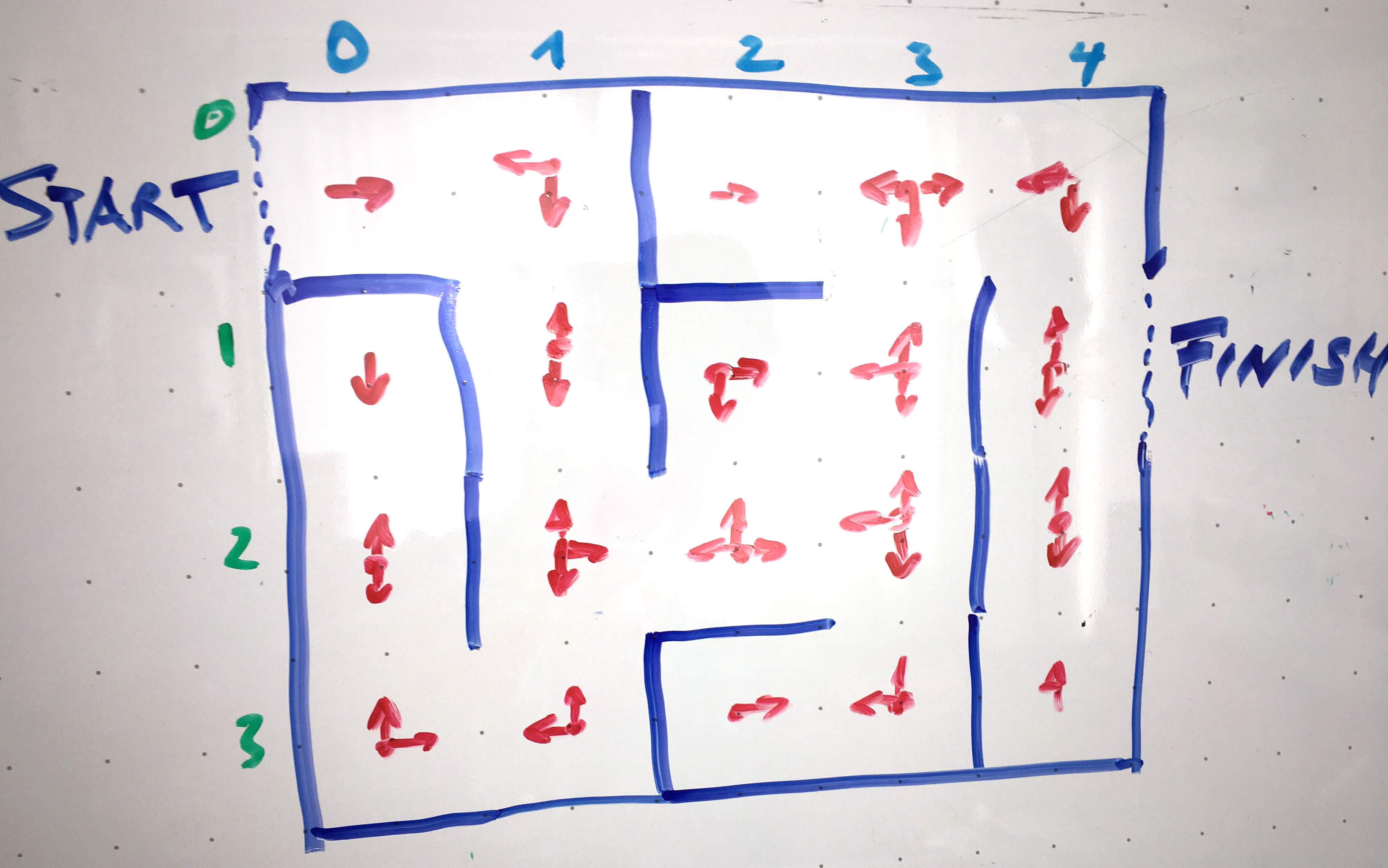
| Abbildung 1: Computer-generiertes 5x4-Labyrinth mit erlaubten Richtungswechseln von Zelle zu Zelle. |
Wie in Abbildung 1 gezeigt, besteht ein Labyrinth aus einer Matrix von MxN Zellen, die jeweils mit Pfeilen in Rot bestimmen, in welche Richtung ein Wanderer sie verlassen darf. Diesen Optionen bestimmen dann die eingezeichneten Wände, die eine Zelle von ihren Nachbarn abschirmt. So bestimmt die Startzelle an den Koordinaten (0, 0), dass aus ihr nur ein Weg in Ostrichtung heraus führt. Daraus schließt der Algorithmus zum Zeichnen des Labyrinths, dass die Ostwand fehlt, während die Südmauer dick1 eingezeichnet wird. Die erlaubten Richtungswechsel definiert das Programm später als North/South/East/West, und wenn eine Zelle "East" angibt muss die rechts von ihr liegende "West" sagen, da der Wanderer das Labyrinth in beiden Richtungen beschreiten darf.
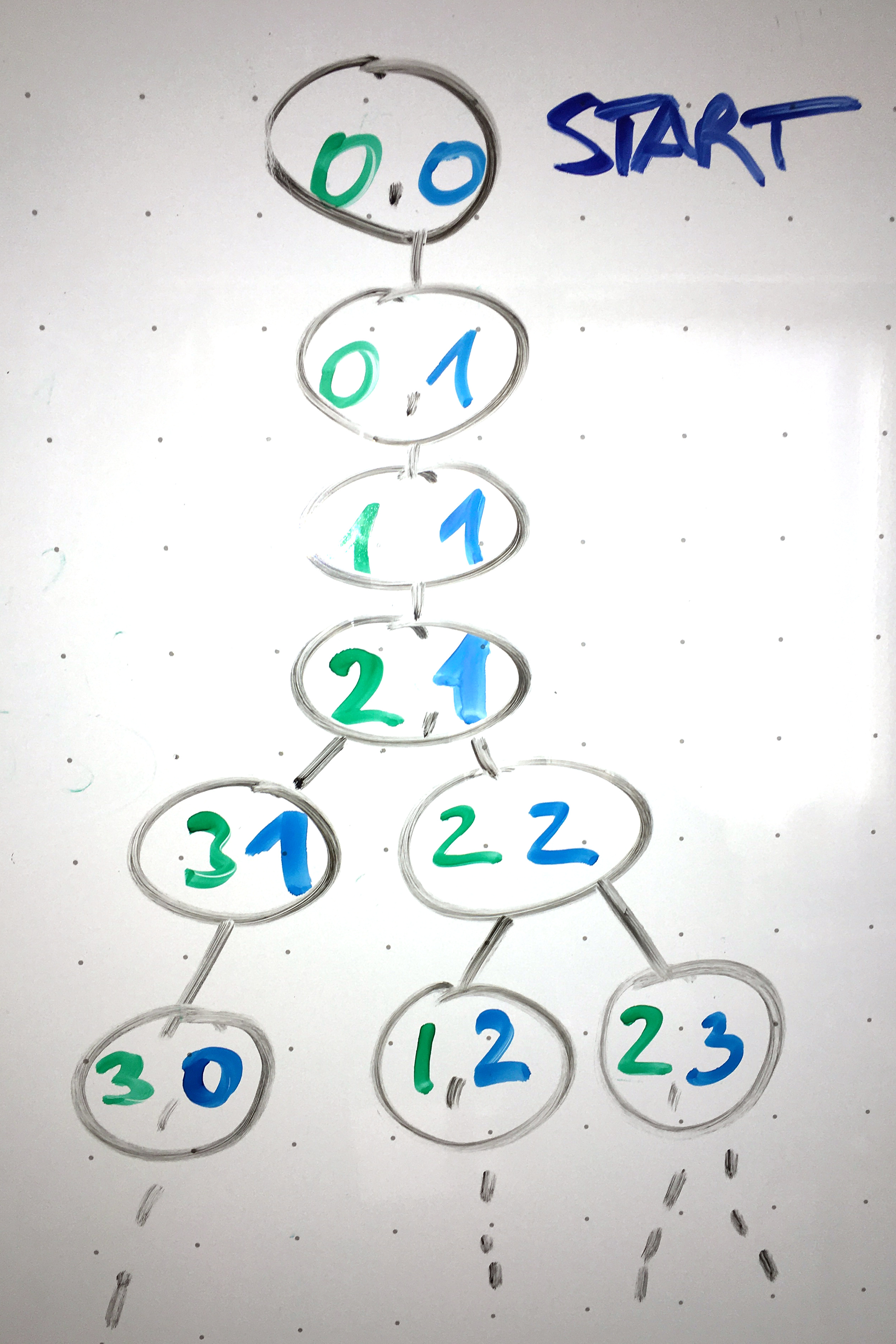 |
| Abbildung 2: Labyrinth als Graph, die Zellen als Knoten und erlaubte Wege als Kanten. |
Die computerinterne Darstellung des Labyrinths als Graphen zeigt Abbildung 2. Vom Startknoten (0, 0) führt nur ein Weg heraus, und zwar zum Knoten (0, 1), der in Abbildung 2 rechts vom Startknoten liegt, die erste Koordinate ist also der Y-Wert, der Zeile bestimmt, die zweite der X-Wert für die Spalte, analog dazu, wie Programme üblicherweise Matrizen speichern.
01 package main
02
03 import (
04 "fmt"
05 "math/rand"
06 "time"
07 )
08
09 const (
10 North = 1 << iota
11 South
12 West
13 East
14 )
15
16 type Cell struct {
17 X, Y int
18 Options int
19 Visited bool
20 Solution bool
21 SolutionPrev *Cell
22 }
23
24 type Maze struct {
25 Cells [][]Cell
26 Width int
27 Height int
28 Start *Cell
29 Finish *Cell
30 }
31
32 var Turns = []int{North, South, West, East}
33
34 func main() {
35 width := 5
36 height := 4
37 rand.Seed(time.Now().UnixNano())
38 maze := newMaze(width, height)
39 maze.Start = &maze.Cells[0][0]
40 maze.Finish = &maze.Cells[height-1][width-1]
41
42 makeMaze(maze)
43
44 solution := maze.Solve()
45 for _, step := range solution {
46 step.Solution = true
47 }
48 fmt.Print(maze.toString())
49 }
Das Hauptprogramm in Listing 1 legt mit newMaze() in Zeile 37 ein neues Labyrinthmodell an, es folgt die Definition von Eingang und Ausgang mit den Zellen ganz links oben und rechts unten. makeMaze() in Zeile 41 wirft den Zufallsgenerator an und baut die Mauern ein, und der Aufruf von Solve() in Zeile 43 findet einen Weg vom Eingang zum Ausgang. Zurück kommt ein Array-Slice von Zellen, die auf diesem Weg durchschritten wurden. Die for-Schleife ab Zeile 45 markiert sie in der internen Darstellung, die Print() in Zeile 47 ins Terminal druckt.
Die restlichen Funktionen in Listing 2 helfen sowohl dem Generator als auch später dem Solver bei der Abarbeitung der Zellen. So hat jede Zelle ein Feld Visited, das Algorithmen auf true setzen, falls sie sie schon bearbeitet haben. Die Funktion Reset() ab Zeile 8 setzt alle Felder der Matrix nach getaner Arbeit wieder zurück auf den ursprünglichen Zustand. Die Funktion Neighbors() ab Zeile 32 gibt alle direkten Nachbarn einer Zelle in allen vier Himmelsrichtungen als Array-Slice von Pointern auf Cell-Typen zurück. Move() ab Zeile 44 schreitet, ausgehend von einer gegebenen Zelle in die angegebene Himmelsrichtung und gibt einen Pointer auf die Zielzelle zurück. Falls der Sprung außerhalb des Matrix-Universums landet, kommt ein Fehler zurück.
Abbildung 3 zeigt drei aufeinanderfolgende Aufrufe des aus den Listings generierten Binaries maze, jedes Mal erzeugt der Algorithmus ein unterschiedliches Labyrinth, und jedes Mal findet der Solver einen Weg vom Eingang zum Ausgang.
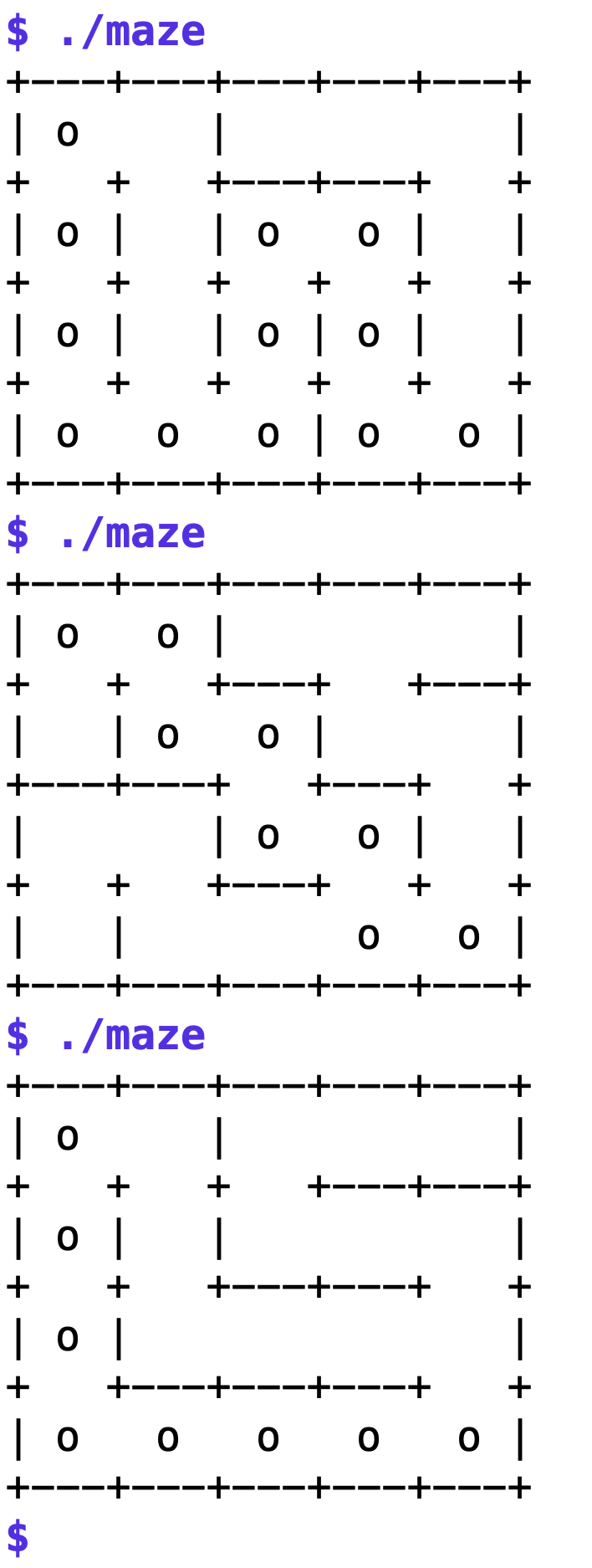 |
| Abbildung 3: Drei verschiedene 5x4-Labyrinthe mit Pfaden vom Start links oben zum Ziel rechts unten. |
Wie entsteht nun so ein computergenerierter Irrgarten? Die meisten Algorithmen hierfür wurden schon vor über 50 Jahren entwickelt, Wikipedia listet die bekanntesten auf ([5]). Für diesen Snapshot kommt das iterative Verfahren zum Einsatz (Abbildung 4).
Listing 1 definiert hierzu ein Labyrinth vom Typ Maze in Zeile 23, mit einem zweidimensionalen Array-Slice von Zellen vom Typ Cell. Außer den Dimensionen der Zellen-Matrix speichert die Struktur auch noch den Start- und den Endpunkt des gesuchten Lösungswegs.
Die Zellen des Labyrints wiederum bestehen, nach ihrer Definition in Zeile 16 aus den X/Y-Koordinaten der Zelle, ihren Pfadoptionen Options und Markern dafür, dass der Algorithmus sie schon abgehandelt hat, oder ob sie Teil des Pfads zur Lösung sind.
 |
| Abbildung 4: Der Algorithmus auf [5], der das Labyrinth generiert. |
Beginnend am Startpunkt arbeitet sich das Programm zu benachbarten Zellen vor, wechselt dabei zufallsbedingt immer wieder die Richtung, und falls es sich in eine Sackgasse hineinmanövriert, in der es keine bisher unbesuchten Zellen als Nachbarn mehr findet, macht es sich auf die Suche nach neuen Kandidaten, die an bereits vorher durchschrittenen Zellen hängen. Alle noch abzuarbeitenden Zellen schiebt makeMaze() in Listing 2 auf einen Stack, von wo es sie später abholt, die Zellennachbarn abklappert, und dort nach neuen Kandidaten sucht.
Dabei knöpft sich Zeile 83 einen zufälligen Nachbarn der aktuell untersuchten Zelle vor, reißt mit cellConnect() die trennende Mauer zu ihm ein und erlaubt anschließend über die Zellenvariable Options Verbindungen in der jeweiligen Himmelsrichtung. Dabei erfahren beide Zellen der Richtung entsprechende Änderungen. Um zum Beispiel eine Verbindung zwischen zwei übereinanderliegenden Zellen einzurichten, erhält die untere Zelle die Option North und die obere Zelle die Option South als gangbaren Weg.
001 package main
002
003 import (
004 "errors"
005 "math/rand"
006 )
007
008 func newMaze(width int, height int) *Maze {
009 var cells [][]Cell
010 for y := 0; y < height; y++ {
011 row := make([]Cell, width)
012 for x := 0; x < width; x++ {
013 row[x].X = x
014 row[x].Y = y
015 }
016 cells = append(cells, row)
017 }
018 return &Maze{
019 Width: width,
020 Height: height,
021 Cells: cells}
022 }
023
024 func (maze *Maze) Reset() {
025 for x := 0; x < maze.Width; x++ {
026 for y := 0; y < maze.Height; y++ {
027 maze.Cells[y][x].Visited = false
028 }
029 }
030 }
031
032 func (maze Maze) Neighbors(cell *Cell) []*Cell {
033 neighbors := []*Cell{}
034 for _, direction := range Turns {
035 tcell, err := maze.Move(cell, direction)
036 if err != nil || tcell.Visited {
037 continue
038 }
039 neighbors = append(neighbors, tcell)
040 }
041 return neighbors
042 }
043
044 func (maze Maze) Move(cell *Cell, turn int) (*Cell, error) {
045 var dx, dy int
046
047 switch turn {
048 case North:
049 dy = -1
050 case South:
051 dy = 1
052 case West:
053 dx = -1
054 case East:
055 dx = 1
056 }
057
058 if cell.X+dx > maze.Width-1 ||
059 cell.X+dx < 0 ||
060 cell.Y+dy > maze.Height-1 ||
061 cell.Y+dy < 0 {
062 return cell, errors.New("Stepped outside")
063 }
064
065 return &maze.Cells[cell.Y+dy][cell.X+dx], nil
066 }
067
068 func makeMaze(maze *Maze) {
069 stack := []*Cell{}
070
071 maze.Start.Options = East
072
073 stack = append(stack, maze.Start)
074 for len(stack) > 0 {
075 lastIdx := len(stack) - 1
076 cur := stack[lastIdx]
077 stack = stack[:lastIdx]
078
079 ncells := maze.Neighbors(cur)
080
081 if len(ncells) > 0 {
082 stack = append(stack, cur)
083 idx := rand.Intn(len(ncells))
084 rcell := ncells[idx]
085
086 rcell.Visited = true
087 cellConnect(cur, rcell)
088 stack = append(stack, rcell)
089 }
090 }
091 }
092
093 func cellConnect(c1 *Cell, c2 *Cell) {
094 if c1.X == c2.X {
095 if c1.Y < c2.Y {
096 c1.Options |= South
097 c2.Options |= North
098 } else {
099 c1.Options |= North
100 c2.Options |= South
101 }
102 }
103
104 if c1.Y == c2.Y {
105 if c1.X < c2.X {
106 c1.Options |= East
107 c2.Options |= West
108 } else {
109 c1.Options |= West
110 c2.Options |= East
111 }
112 }
113 }
Um in Go das letzte Element von einem Array-Slice zu entfernen und in einer Variable abzulegen wie ab Zeile 75 in Listing 2, sind erstaunlich viele Schritte nötig. Skriptsprachen wie Python machen das ratzfatz mit pop(), aber Go besteht darauf, erst den letzten Index des Arrays anzusprechen (len(slice)-1), den dortigen Wert abzuholen, und anschließend das Teil-Slice, das sich von den Indexnummern 0 bis len(slice)-1 (ausschließlich, also ohne das letzte Element!) erstreckt, wieder der Slice-Variablen zuzuweisen:
last = slice[len(slice)-1]
slice = slice[:len(slice)-1]Wegen Gos interner Slice-Arithmetic, die nur Pointer verschiebt, aber keine Elemente umkopiert, ist das Ganze sehr effizient, aber im Programmcode halt doch nicht ganz einfach zu lesen.
Um eine Reihe von Optionen effizient in einer Integer-Variablen abzulegen, definiert Listing 1 die Himmelsrichtungen als Konstanten. Das Schlüsselwort iota mit dem Operator << in Zeile 10 von Listing 1 setzt die Werte der Konstanten North, South, West und East als Zweierpotenzen, also auf die Werte 1, 2, 4 und 8.
Damit ist es möglich, eine Variable (wie zum Beispiel Options) durch binäres Odern auf mehrere dieser Werte zu setzen. Soll eine Zelle zum Beispiel Übergänge sowohl nach Norden als auch Osten zulassen, stellt das Programm ihren Wert auf 1 | 8 ein, also 9. Will es später testen, ob Norden eine Option ist prüft es Option & 8, was immer dann ungleich Null ist, falls vorher eine 8 hineinge-odert wurde.
Beim zufällig Auswählen von Elementen aus einem Array-Slice wie in Zeile 83 von Listing 2 gilt es aufzupassen wie ein Luchs, damit der Zugriff auch wirklich zufällig erfolgt und nicht etwa manche Elemente bevorzugt erscheinen. Die Funktion Intn(x) aus dem Standardpaket "math/rand" liefert hierzu gleichverteilte Zufallswerte in Form einer Ganzzahl zwischen 0 (einschließlich) und dem Integerwert x (ausschließlich):
idx := rand.Intn(len(slice))
randElement := slice[idx]Im Codestück oben liefert len(slice) die Anzahl der Elemente im Array, der Index des letzten Elements ist aber Eins weniger. Also liefert der Zufallsgenerator gleichverteilte Indexwerte zwischen 0 und len(slice)-1, jeweils einschließlich -- genau das vom Doktor verordnete Medikament zur Auswahl eines zufälligen Array-Elements.
Was passiert, wenn der Zufallsgenerator keine rein zufälligen Werte ausspuckt, sondern in eine Richtung tendiert, also Vorlieben hat (Bias), zeigt Abbildung 5: Öde Labyrinthe, die kein Mensch anpacken würde, aber der Computer macht natürlich trotzdem einen guten Job.
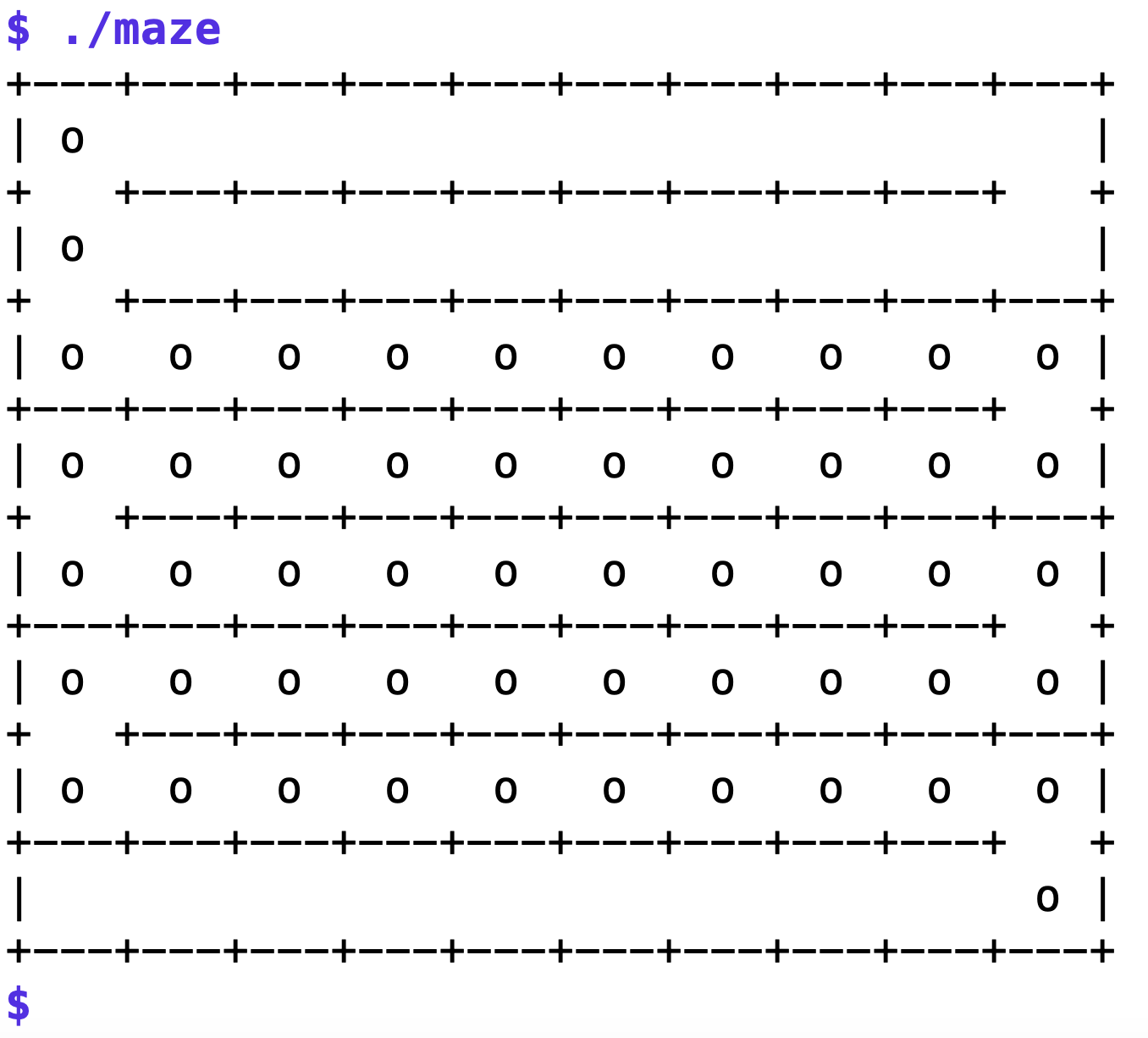 |
| Abbildung 5: Ein defekter Zufallsgenerator mit Vorlieben generiert nur langweilige Labyrinthe. |
Damit der Generator nicht bei jedem erneuten Programmlauf das gleiche Labyrinth generiert, muss main() ihn auf einen Wert initialisieren, der von Aufruf zu Aufruf unterschiedlich ist. Zeile 36 in Listing 1 setzt ihn deswegen mittels rand.Seed() auf die aktuelle Uhrzeit in Nanosekunden, die auf ein relativ breites Spektrum streut.
Dass der Algorithmus zum Generieren nur den Startpunkt erhält und scheinbar keinen Endpunkt des Labyrints braucht, liegt daran, dass das Verfahren Wege generiert, auf denen der Wanderer alle Punkte des Irrgartens erreichen kann. Das Verfahren stellt sicher, dass keinerlei abgeschottete Sektionen entstehen. Insofern ist garantiert, dass der Solver später jeden wahlfrei definierten Endpunkt erreichen wird. Endlosschleifen beherrscht er ebenfalls nicht, da er niemals auf bereits vorher beschrittene Wege einbiegt, wer solche Irrgärten möchte, findet eine breite Palette weiterer Algorithmen, die sich ebenfalls einfach implementieren lassen.
Um das Labyrinth auf den Bildschirm zu malen, kann das Programm entweder eine Grafikbibliothek bemühen oder im einfachsten Fall Zeichen per ASCII-Art ins Terminal schreiben. Da einzelne Zellen im Labyrinth ihre Mauern mit den Nachbarzellen teilen, brauchen sie sich nicht um die Darstellung aller ihrer vier Wände zu bemühen, sondern lediglich um zwei, den Rest erledigen die nördlichen und westlichen Nachbarn.
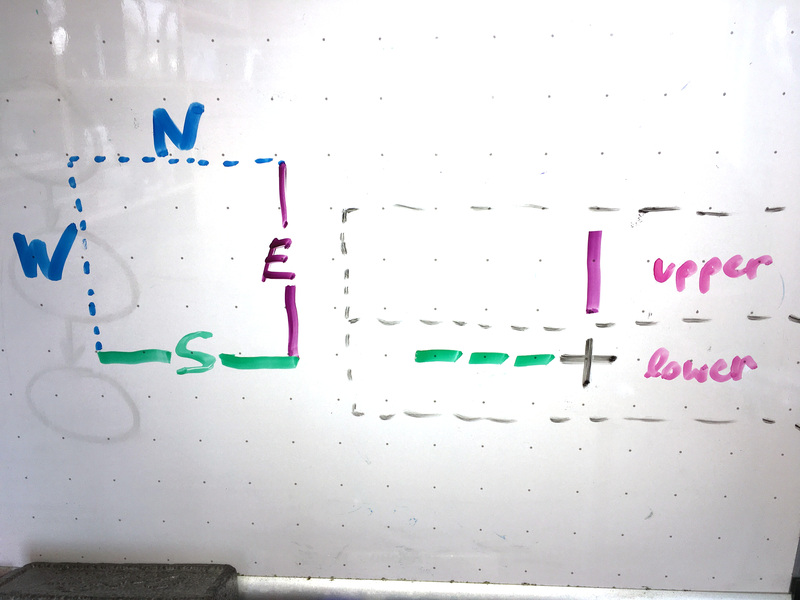 |
| Abbildung 6: Eine Zelle kümmert sich nur um die Darstellung ihrer östlichen und südlichen Mauern, alles andere machen die Nachbarzellen. |
Der Algorithmus zum Malen des Labyrinths muss also wie in Listing 3 von links nach rechts und von oben nach unten durch die Zellen der internen Darstellung fahren, und bei jeder Zelle unten eine Wand einziehen, falls die Zelle in Richtung South offen steht, und rechts eine Wand, falls East eine Option ist. Befindet sich eine Zellwand am Rand des Labyrinths, also ganz links, rechts, oben oder unten, sind in diesen Richtungen aber ebenfalls Mauern anzubringen.
01 package main
02
03 func (maze Maze) toString() string {
04 output := ""
05
06 for x := 0; x < maze.Width; x++ {
07 output += "+---"
08 }
09 output += "+\n"
10
11 for y := 0; y < maze.Height; y++ {
12 upper := "|"
13 lower := "+"
14 for x := 0; x < maze.Width; x++ {
15 wall := "|"
16 if (maze.Cells[y][x].Options & East) != 0 {
17 wall = " "
18 }
19 sol := " "
20 if maze.Cells[y][x].Solution {
21 sol = "o"
22 }
23 upper += " " + sol + " " + wall
24
25 wall = "---"
26 if (maze.Cells[y][x].Options & South) != 0 {
27 wall = " "
28 }
29 lower += wall + "+"
30 }
31 output += upper + "\n"
32 output += lower + "\n"
33 }
34
35 return output
36 }
Dabei besteht jede Zellenzeile, wie aus Abbildung 5 ersichtlich, aus drei ASCII-Zeilen und vier -Spalten. Die unterste Zeile enthält bei einer geschlossenen Südwand den String "+---+", ist sie offen, steht dort "+ +". Bei einer geschlossenen Ostwand steht in der zweiten Zeile von oben das Pipe-Zeichen |, bei einer offenen Wand statt dessen ein Leerzeichen. Um die Nord- und Westwände braucht sich die Zelle, wie gesagt, nicht zu kümmern, das erledigen die Süd- bzw. Ostwände ihrer Nachbarzellen ordnungsgemäß.
Steht das Labyrinth nach dem Aufruf von makeMaze() in Zeile 41 von Listing 1 fest, sucht die Funktion Solve() in Listing 4 nach einer Lösung, um vom Start- zum Zielpunkt zu gelangen.
01 package main
02
03 func (maze Maze) Solve() []*Cell {
04 maze.Reset()
05 stack := []*Cell{maze.Start}
06
07 for len(stack) > 0 {
08 cur := stack[len(stack)-1]
09 cur.Visited = true
10
11 if cur.X == maze.Finish.X &&
12 cur.Y == maze.Finish.Y {
13 return stack
14 }
15
16 var moveto *Cell
17 for _, turn := range Turns {
18 if (cur.Options & turn) != 0 {
19 trycell, err := maze.Move(cur, turn)
20 if err == nil && !trycell.Visited {
21 moveto = trycell
22 break
23 }
24 }
25 }
26
27 if moveto == nil {
28 // nowhere to go, backtrack
29 stack = stack[:len(stack)-1]
30 continue
31 }
32
33 stack = append(stack, moveto)
34 }
35
36 return stack
37 }
Der Solver sucht Depth-First, dringt also erstmal in die Tiefe vor, um mit einem Schnellschuss eine Lösung zu finden, statt an jeder Abzweigung alle Möglichkeiten durchzuprobieren, um so am Ende auf dem kürzesten Weg ins Ziel zu gelangen (Breadth-First).
Führen manche Wege im Labyrinth im Kreis, stellt das primitive Solver vor erschwerte Herausforderungen, denn sie dürfen sich nicht festfressen, indem sie ewig im Kreis rennen. Unser Solver Solve() hingegen wäre gegen das Problem gewappnet, denn er markiert bereits bearbeite Zellen im Feld Visited und würde nie auf die Idee kommen, eine davon nochmals zu behandeln.
Der Solver prescht also, vom Startpunkt aus, entlang erlaubter Pfade, nimmt jeweils die erstbeste Abzweigung und schiebt die korrespondierende Zelle auf den Stack stack. Kommt er zufällig am Zielpunkt vorbei, sagt er die Jagd ab und beendet sich siegreich, mit den auf dem Stack aufgestapelten Zellen als Lösungsweg. Das ist nicht unbedingt der kürzeste Pfad zur Lösung, aber der Algorithmus hat ihn zumindest schnell gefunden. Kommt er hingegen nicht am Labyrinthende sondern am Ende einer Sackgasse an, muss er sich an seinem eigenen Stack zurückhangeln, um zurück zu einer vorher genommenen Abzweigung zu kommen, und dort auf alternativen Pfaden zu forschen. Irgendwann wird er so am Ziel vorbeikommen, und den bis dahin aufgebauten Stack als Lösungweg zurück an den Aufrufer geben. Das Hauptprogramm markiert mit diesen Daten die Zellen entlang des Weges, indem es jeweils deren Flag Solution auf einen wahren Wert setzt, und die Druckfunktion schreibt in solche Zellen ein "o" hinein.
Alle vier Listings dieser Ausgabe kompiliert das Kommando
$ go build maze.go print.go solve.go manip.gin ein Binary maze, das beim Aufruf ein 5x4-Labyrinth samt Lösung ausspuckt. Die Dimensionen lassen sich leicht über die Werte für width und height in main() verändern, und auch das Ausprobieren unterschiedliche Algorithmen zum Generieren und Lösen neuer aufregender Labyrinthe sei interessierten Bastlern nahegelegt.
Listings zu diesem Artikel: http://www.linux-magazin.de/static/listings/magazin/2021/01/snapshot/
"Labyrinth", https://de.wikipedia.org/wiki/Labyrinth
"Mazes for Programmers", Jamis Buck, 2015, https://www.amazon.com/dp/B013HA1UY4
Go-Projekt auf Github zum Erstellen und Lösen von Labyrinthen: https://github.com/itchyny/maze
"Maze generation algorithm", Wikipedia, https://en.wikipedia.org/wiki/Maze_generation_algorithm
"Maze solving algorithm", Wikipedia, https://en.wikipedia.org/wiki/Maze_solving_algorithm
Hey! The above document had some coding errors, which are explained below:
Unknown directive: =desc
Unterminated C<...> sequence