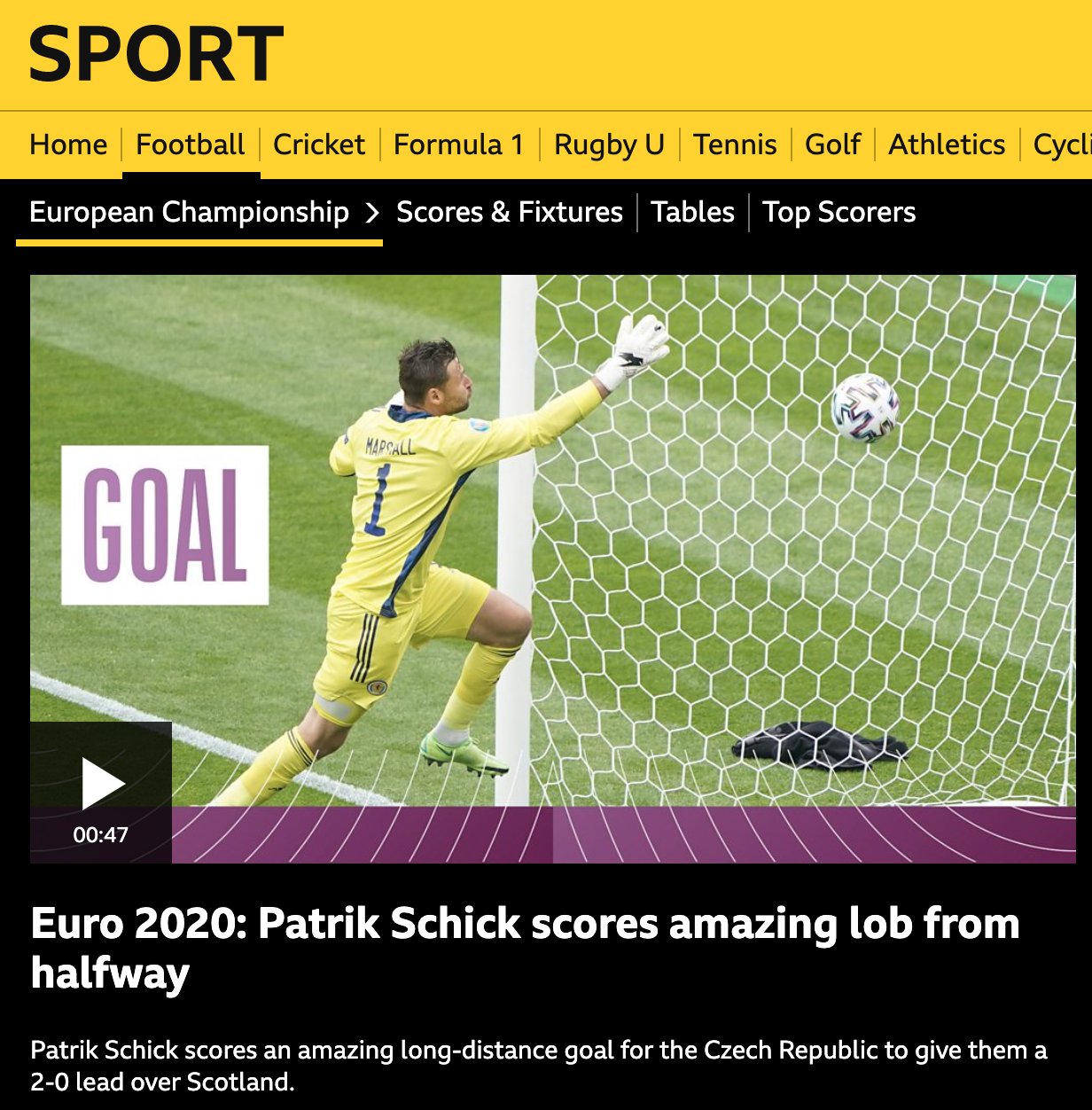
Die Fußball-EM vor einem Jahr war ja ein ziemlicher Reinfall für Jörgi Löws Gurkentruppe, aber eine Szene des Spiels Tschechien gegen Schottland ist trotzdem bis heute in meiner Erinnerung haften geblieben: Da war der Torwart der Schotten weit aus dem Tor herausgelaufen, der Spieler Patrick Schick der Tschechen bemerkte dies an der Mittellinie stehend, und schlenzte in einem sehenswerten Bogenschuß den Ball ins Gehäuse des aushäusigen Torwarts. Seit dieser Zeit habe ich immer wieder versucht, diese Szene auf meiner Positon als Knipser der Amateurmannschaft "Beer Fit" in San Francisco zu replizieren, aber bislang leider ohne Erfolg. Ich beschloss deshalb, daraus ein in Go geschriebenes Videospiel für die Snapshot-Kolumne zu machen.
 |
| Abbildung 1: Bei dem sagenhaften Lüpfertor während der EM 2020 sah der schottische Torwart nur noch dem Ball hinterher. |
Das zugrundeliegende physikalische Modell für den Lüpfer-Schuss nennt sich "Schiefer Wurf" und wird in jedem guten Schulphysikbuch heruntergebetet. Das weiß ich zufällig ganz genau, denn während meines Elektrotechnik-Studiums an der TU München schwitzte ich durch manche Prüfung im Mörderfach "Technische Mechanik". Und auch viele viele Jahre später, mit zitternden Händen ein total vergilbtes Diplom haltend, brauchte ich nur einen kurzen Auffrischer, um die Formeln für die Ballposition abhängig vom Startpunkt, des Abschußwinkels und der -geschwindigkeit, sowie der verstrichenen Zeit herzuleiten.
Die Flugbahn des Fußballs, der weit über dem Kopf des herausgeeilten Torwarts in hohem Bogen ins dahinterliegende Tor fliegt, ist keineswegs der einzige Anwendungsfall des schiefen Wurfs. Dieselbe Formel errechnet auch die Flugbahnen ballistischer Geschosse, von der Kanonenkugel bis zur Mittelstreckenrakete, und ist deshalb seit Urzeiten bekannt.
 |
| Abbildung 2: Klassisches Lüpfer-Tor: Der Ball fliegt über den Torwart und purzelt ins Tor hinein. |
Damit die Formel für die Flugbahn in X/Y-Koordinaten in Abhängigkeit von der verstrichenen Zeit (Abbildung 3) simpel bleibt, berücksichtigt die Implementierung im Video-Spiel nur die Anfangsgeschwindigkeit, mit der der Angreifer den Ball in die Luft kickt, den Abschusswinkel, sowie die Gravitation, die den Ball auf der Bogenbahn wieder zur Erde zurückholt. Sie vernachlässigt den Luftwiderstand des Balls in der Atmosphäre. Den könnte man mit unterschiedlichen Strömungsmodellen einarbeiten, aber dann dürfte auch eventueller herrschender Gegen- oder Rückenwind eine Rolle spielen, und sogar die atmosphärischen Bedingungen, wie Nebel oder Nieselregen. Deshalb nimmt das Programm später einfach an, dass der Ball Vakuum fliegt, schließlich geht nur ums Prinzip, nicht um Genauigkeit ([7]).
 |
| Abbildung 3: Formel für X/Y-Koordinaten auf der Wurfparabel, abhängig von der verstrichenen Zeit (Quelle: Wikipedia) |
01 package main
02
03 import (
04 "math"
05 )
06
07 func chipShot(v float64, a float64, t float64) (float64, float64) {
08 const g = 9.81
09
10 x := v * t * math.Cos(a)
11 y := v*t*math.Sin(a) - g/2*t*t
12
13 if y < 0 {
14 y = 0
15 }
16
17 return x, y
18 }
Listing 1 setzt die Formel in Go-Code um und packt sie in die Funktion chipShot(), die als Eingabeparameter die Abschussgeschwindikgeit, den Winkel im Radiant-Format und die verstrichene Zeit in Sekunden entgegen nimmt. Zurück kommt die Position des Balles zum gegebenen Zeitpunkt auf der Bogenbahn, als X- und Y-Wert. Da die Formel für die Y-Koordinate auf der Flugbahn blind negative Werte liefert, die Erdoberfläche aber einem Fußball keinen Eintritt in den Untergrund gewährt, setzt Zeile 14 den Höhenwert auf Null falls die Flugparabel negative Werte annimmt.
Zu Testzwecken plottet Listing 2 mittels Gos Standard-Plotter plot die Flugroute des Balls bei verschiedenen Ausgangsparametern in ein X/Y-Koordinatensystem und erzeugt eine PNG-Datei nach Abbildung 4. Die rote Flugbahn zeigt den Ball nach dem Abschuss des Balls mit 10 Meter pro Sekunde und einem Anstellwinkel von 45 Grad. Tritt der Stürmer beherzter rein, und der Ball startet mit 15 m/s bei gleichem Winkel, fliegt der Ball entsprechend der grünen Kurve höher in die Luft und legt auch eine weitere Entfernung zurück bevor er wieder zur Erde zurückkommt. Die blaue und die gelbe Kurve zeigen Flugbahnen, mit geringerem beziehungsweise höherem Anstellwinkel, was in unterschiedlich ausgeprägten Höhenflügen aber der gleichen waagrecht zurückgelegten Strecke resultiert. Den Abschusswinkel definieren die Zeilen 19-22 in Listing 2 jeweils nicht im Grad- sondern im Radiant-format, genau wie ihn die Sinus- und Cosinus-Funktionen des math-Pakets in Go erwarten. Da 180 Grad dem Wert Pi entsprechen, muss die Funktion nur die entsprechenden Bruchteile ausrechnen, so werden aus 45 Grad Pi-Viertel, und aus 30 Grad ein sechstel Pi.
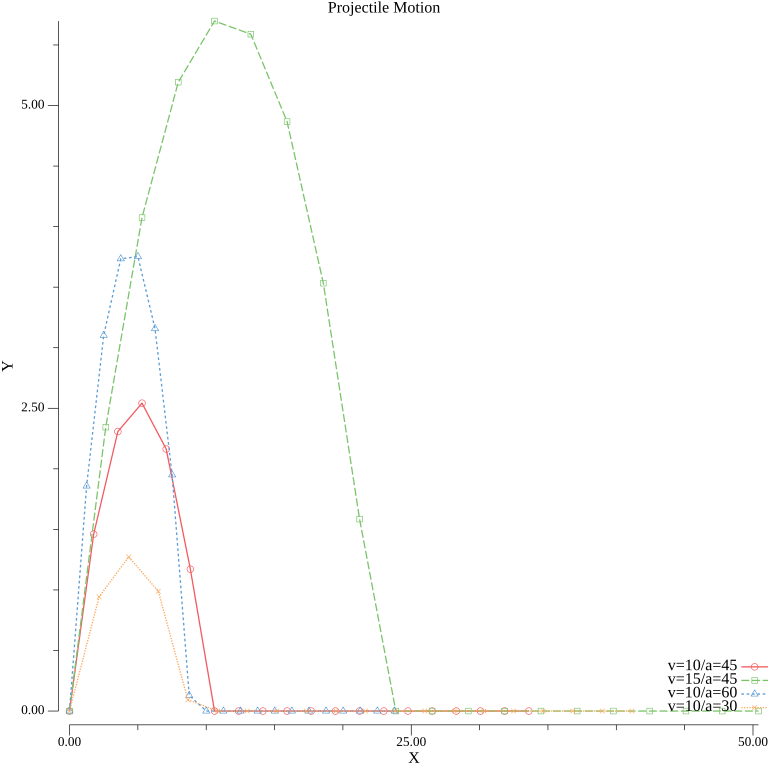 |
| Abbildung 4: Wurfparabel für unterschiedliche Ballwinkel und Anfangsgeschwindigkeit |
01 package main
02
03 import (
04 "gonum.org/v1/plot"
05 "gonum.org/v1/plot/plotter"
06 "gonum.org/v1/plot/plotutil"
07 "gonum.org/v1/plot/vg"
08 "math"
09 )
10
11 func main() {
12 p := plot.New()
13
14 p.Title.Text = "Projectile Motion"
15 p.X.Label.Text = "X"
16 p.Y.Label.Text = "Y"
17
18 err := plotutil.AddLinePoints(p,
19 "v=10/a=45", shoot(10, math.Pi/4),
20 "v=15/a=45", shoot(15, math.Pi/4),
21 "v=10/a=60", shoot(10, math.Pi/3),
22 "v=10/a=30", shoot(10, math.Pi/6),
23 )
24 if err != nil {
25 panic(err)
26 }
27
28 err = p.Save(8*vg.Inch, 8*vg.Inch, "curve.png")
29 if err != nil {
30 panic(err)
31 }
32 }
33
34 func shoot(v float64, a float64) plotter.XYs {
35 n := 20
36 pts := make(plotter.XYs, n)
37
38 t := 0.0
39 for i := range pts {
40 pts[i].X, pts[i].Y = chipShot(v, a, t)
41 t += 0.25
42 }
43 return pts
44 }
Zu jedem Graphen definiert die ab Zeile 34 in Listing 2 implementierte Funktion shoot() jeweils 20 Zeitpunkte im Abstand von 0,25 Sekunden, berechnet die mit chipShot() aus Listing 1 die X/Y-Koordinaten die aktuelle Ballposition und speichert die Messpunkte in einem Array namens pts vom Typ plotter.XYs, den sie nach Abschluss der for-Schleife wieder ans Hauptprogramm zurück reicht. Letzteres schiebt die Daten mittels AddLinePoints an den Plotter weiter, der nicht nur eine sondern gleich vier solcher Datensätze als Kurven mitsamt Legende ins Koordinatensystem zeichnet, bis Save() in Zeile 28 die Graphik als .png-Datei 8x8 Inches groß abspeichert.
Diese physikalischen Grundlagen der ballistischen Flugbahn verpacken die restlichen Listings dieser Ausgabe in ein Desktop-Spiel namens chipshot (der englischen Bezeichnung des Bogenlampen-Schusses im Fußball). Abbildung 5 zeigt, wie der User mit dem oberen Regler eine Startgeschwindigkeit des Balles von 15 m/s eingestellt hat, mit dem unteren einen Abschusswinkel von 45 Grad. Den Torwart symbolisiert das lachsfarbene Rechteck unten Mitte, das Fußballtor der grüne Quader weiter rechts. Mit den eingestellten Parametern fliegt der Ball, nachdem der User den Button "Shoot" links oben gedrückt hat, knapp über den Torwart hinweg und rollt mit letzter Kraft ins Tor. Aber das klappt nicht immer, Abbildung 6 zeigt zum Beispiel einen Versuch, bei dem der Ball zwar über den Torwart hinwegfliegt, aber dann auf dem Weg zum Tor verhungert, da er nicht genug Bewegungsenergie mitgebracht hat und nach dem Aufschlag am Boden wegen Reibung vorzeitig ausrollt. Und in Abbildung 7 schließlich kommt der Ball vorzeitig herunter und der Torwart fängt ihn ab. Game over!
 |
| Abbildung 5: Das fertige Lüpferspiel: der Ball fliegt über den der Torwart hinweg und rollt ins Tor. |
Simple Videospiele dieser Art hielten in den 80ern des letzten Jahrhunderts erstmals Einzug in sogenannte Spielhallen, in denen Riesenkästen mit eingebauten Bildschirmen standen, in deren Münzschlitze User Münzen steckten, und sich damit das Recht erkauften, das eingebaute Spiel mittels Joystick und Feuerknopf ein paar Minuten traktieren zu dürfen. Jüngere Leser reiben sich verwundert die Augen und fragen, ob damals noch keine Spielkonsolen in den Wohnzimmern der Leute standen!
 |
| Abbildung 6: Zu schwach geschossen: Hier verhungert Ball hinter dem Torwart auf dem Weg zum Tor. |
Die Konzepte dieser Spiele und das Erstellen von Programmen, die sie ermöglichen, erklärt schön das Buch "Classic Game Design" von Franz Lanzinger ([4]), einem Pionier der Technik, der laut eigener Aussage einmal auf der Touristenmeile der kalifornischen Stadt Santa Cruz einen Automaten mit dem damals populären Videospiel "Crystal Castles" ([8]) fand, und mit Hilfe der ihm bekannten Kombination der beiden Feuerknöpfe herausfand, dass Besucher des Vergnügungsparkes während der Lebensdauer des Automaten sage und schreibe 100.000 Quarters (Vierteldollar-Münzen) hineingesteckt hatten. Hochmultipliziert auf die damals produzierte Stückzahl von 5.000 Automaten ergeben sich daraus (recht optimisch geschätzte) Gesamteinnahmen des Spiels von 100 Millionen Dollars ([5]). Ah, ja, die gute alte Zeit.
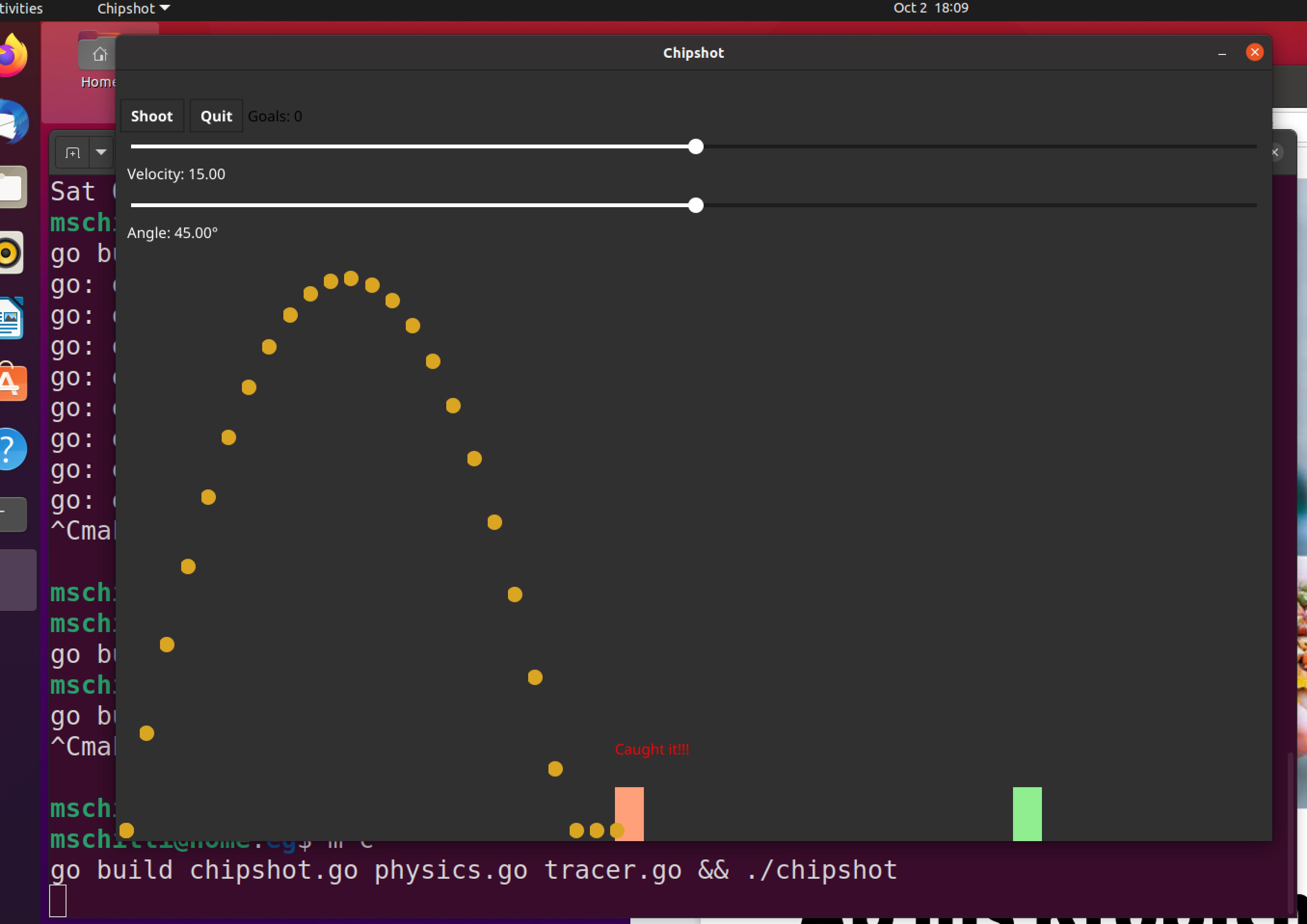 |
| Abbildung 7: Zu kurz geschossen! Der Torwart hat den Ball gefangen. Game over. |
Allen Videospielen ist gemein, dass der Rechner die mehr oder weniger flüssig dargestellten Bewegungen mehrmals pro Sekunde in sogenannten Frames ausrechnet und anzeigt. Videospiele basieren meist auf fertigen Engines, die die Darstellung übernehmen und der Applikation Zugriff auf das Spielgeschehen gewähren, in dem sie zu jedem Frame eine Callback-Funktion anspringen, in der der Spieleprogrammierer dann seine Spielfiguren voranschiebt oder prüft, ob sie mit aufgestellten Hindernissen kollidieren.
Ein Mensch, dessen Gehirn scheinbar spielerisch den Überblick über eine komplexe Situation auf dem Bildschirm behält, bekommt irgendwie automatisch sofort mit, falls sich der Ball auf dem Video-Spielfeld dem Torwart oder dem Tor nähert. Ein Programm ist hingegen darauf angewiesen, in jedem Spiel-Frame wieder und wieder manuell zu testen, ob der Ball denn tatsächlich schon an einem der überwachten Objekte angeschlagen ist. Das Programm kann das zwar rasend schnell, und deswegen sieht es so aus, als besäße es eine ähnliche Mustererkennung, aber das Verfahren basiert auf einer Illusion.
Das unten vorgestellte Video-Spiel "Chipshot" (nach dem englischen Begriff des Bogenschusses im Fußball) besteht aus reinem Go-Code, und als Grafik-Library nutzt es das plattformunabhängige Fyne-Projekt, das schon letzten Monat im letzten Snapshot mit einem Fotosortierer auftrumpfte. Die Abbildungen 5-7 zeigen das Spiel in Aktion. Der User stellt über die beiden weißen Regler oben links die Startgeschwindigkeit des Balles zwischen 0 und 30, und den den Anstellwinkel zwischen 0 und 90 Grad ein. Klickt er dann mit der Maus auf den Shoot-Button links oben, fängt der Ball auf seiner parabelartigen Bahn an zu fliegen. Sobald er wieder auf dem Boden aufschlägt, rollt er noch eine zeitlang aus, und kullert mit etwas Glück ins Tor hinein, was den Zähler "Goals" oben um eins erhöht. Kommt er allerdings schon vor dem Torwart herunter, fängt ihn dieser ab und lacht schadenfroh, weil es dafür keinen Punkt gibt. Gleiches gilt, falls der Angreifer zu stark draufballert, und der Ball übers Tor fliegt, oder nicht genugt Schmackes mitgibt, sodass der Ball auf dem Weg zum Tor verhungert.
Punktet der Spieler, erhöht sich der Torzähler, und das Spiel erzeugt eine neue Situation, indem es Torwart und Tor umstellt. Versagt der Angreifer und der Ball geht nicht ins Tor, darf der Spieler die gleiche Situation noch einmal mit unterschiedlichen Reglereinstellungen probieren, aber das Spiel stellt den Torzähler zur Strafe auf Null zurück.
Listing 3 baut das Spiel auf. Damit nach einem Neustart des Programms nicht immer die gleiche Ausgangsposition hochkommt, setzt Zeile 37 mit rand.Seed() den Go-internen Zufallsgenerator auf einen Wert, der mit den Nanosekunden der aktuellen Uhrzeit ziemlich weitgestreute Ausgangsdaten liefert.
001 package main
002
003 import (
004 "fmt"
005 col "golang.org/x/image/colornames"
006 "image/color"
007 "math/rand"
008 "os"
009 "time"
010
011 "fyne.io/fyne/v2"
012 "fyne.io/fyne/v2/app"
013 "fyne.io/fyne/v2/canvas"
014 "fyne.io/fyne/v2/container"
015 "fyne.io/fyne/v2/data/binding"
016 "fyne.io/fyne/v2/widget"
017 )
018
019 type UI struct {
020 ball, goal, goalText, goalie,
021 goalieText fyne.CanvasObject
022 }
023
024 var (
025 gameWidth = float32(1200)
026 gameHeight = float32(800)
027 goalWidth = float32(30)
028 goalHeight = float32(60)
029 minDist = 30
030 textHover = float32(50)
031 )
032
033 func main() {
034 a := app.New()
035 ui := UI{}
036
037 rand.Seed(time.Now().UnixNano())
038
039 w := a.NewWindow("Chipshot")
040 w.Resize(fyne.NewSize(gameWidth, gameHeight))
041 w.SetFixedSize(true)
042
043 goalieDist, goalDist := itemsXPos()
044 ui.goalie = canvas.NewRectangle(col.Lightsalmon)
045 ui.goalie.Move(fyne.NewPos(goalieDist, gameHeight-goalHeight))
046 ui.goalie.Resize(fyne.NewSize(goalWidth, goalHeight))
047
048 ui.goal = canvas.NewRectangle(col.Lightgreen)
049 ui.goal.Move(fyne.NewPos(goalDist, gameHeight-goalHeight))
050 ui.goal.Resize(fyne.NewSize(goalWidth, goalHeight))
051
052 ui.ball = canvas.NewCircle(col.Red)
053 ui.ball.Move(fyne.NewPos(0, gameHeight-30))
054 ui.ball.Resize(fyne.NewSize(15, 30))
055
056 ui.goalText = canvas.NewText("Goal!!!", col.Red)
057 placeTextHover(ui.goalText, ui.goal)
058
059 ui.goalieText = canvas.NewText("Caught it!!!", col.Red)
060 placeTextHover(ui.goalieText, ui.goalie)
061
062 play := container.NewWithoutLayout(ui.goal, ui.goalie, ui.ball, ui.goalText, ui.goalieText)
063
064 velo := binding.NewFloat()
065 veloSlide := widget.NewSliderWithData(0, 30, velo)
066 formVelo := binding.FloatToStringWithFormat(velo, "Velocity: %0.2f")
067 veloLabel := widget.NewLabelWithData(formVelo)
068 veloSlide.SetValue(15)
069
070 angle := binding.NewFloat()
071 angleSlide := widget.NewSliderWithData(0, 90, angle)
072 formAngle := binding.FloatToStringWithFormat(angle, "Angle: %0.2f°")
073 angleLabel := widget.NewLabelWithData(formAngle)
074 angleSlide.SetValue(45)
075
076 countText := canvas.NewText("Goals: 0", &color.Black)
077 count := 0
078
079 shoot := widget.NewButton("Shoot", func() {
080 v, _ := velo.Get()
081 a, _ := angle.Get()
082 success := animate(v, a, ui)
083 if success {
084 count++
085 goalieDist, goalDist := itemsXPos()
086 ui.goalie.Move(fyne.NewPos(goalieDist, gameHeight-goalHeight))
087 ui.goal.Move(fyne.NewPos(goalDist, gameHeight-goalHeight))
088 placeTextHover(ui.goalieText, ui.goalie)
089 placeTextHover(ui.goalText, ui.goal)
090 } else {
091 count = 0
092 }
093 countText.Text = fmt.Sprintf("Goals: %d", count)
094 countText.Refresh()
095 // return ball to origin
096 ui.ball.Move(fyne.NewPos(0, gameHeight-30))
097 })
098
099 quit := widget.NewButton("Quit",
100 func() { os.Exit(0) })
101
102 buttons := container.NewHBox(shoot, quit, countText)
103
104 con := container.NewVBox(play, buttons, veloSlide,
105 veloLabel, angleSlide, angleLabel)
106
107 w.SetContent(con)
108 w.ShowAndRun()
109 }
110
111 func randRange(from, to int) float32 {
112 return float32(rand.Intn(to-from+1) + from)
113 }
114
115 func itemsXPos() (float32, float32) {
116 d1 := randRange(minDist, 2*int(gameWidth)/3)
117 d2 := randRange(int(d1)+minDist, int(gameWidth-goalWidth))
118 return d1, d2
119 }
Die verwendeten UI-Elemente definiert die Struktur vom Typ UI in Zeile 19, darin finden der Fußball, das Tor, der Torwart, sowie die über dem Tor bzw. Torwart dargestellten Texte Platz. Die globalen Variablen im Block ab Zeile 24 legen Dimensionen des Spielfelds und der Spielfiguren fest. Die Hauptfunktion main() ab Zeile 33 erzeugt erst eine neue Fyne-Applikation, definiert ein Fenster, und setzt es auf eine fixe Größe. Tor und Torwart stellt sie durch Fyne-Rechtecke in den Farben hellgrün und lachsfarben dar. Die Funktion itemsXPos(), die ab Zeile 115 definiert ist liefert Positionen für Tor und Torwart, sowohl beim Programmstart als auch nach dem Meistern einer Standardsituation. Sie stellt sicher, dass keine unsinnigen Konstellationen entstehen, wie dass der Torwart zum Beispiel hinter dem Tor steht.
Wenn der Torwart einen Ball abfängt oder es im Tor schnackelt, kommt über diesen Spielfiguren eine Schrift hoch, die das Ereignis dreimal blinkend meldet. Die zugehörigen graphischen Widgets definieren die Zeilen 56 und 59, die Funktion placeTextHover() (später in Listing 4 definiert) stellt jedoch anfangs sicher, dass sie sich zunächst mit Hide() verstecken, und erst später sorgt die Funktion blink() bei Bedarf dafür, dass sie ihren Text mehrmals aufblitzen lassen.
Der Ball liegt as Kreis-Widget vor, den Zeile 52 anlegt und mit roter Farbe füllt. Er startet an X-Position 0, also am linken Spielfeldrand. Alle diese Widgets verpackt Zeile 62 in den Spielfeld-Container play, den später Zeile 104 unter die Knöpfe und Regler platziert, mit denen der User das Spielgeschehen beeinflussen kann.
Die beiden Regler velo und angle lassen sich mit der Maus verschieben und durch durch Fynes Binding-Schnittstelle zeigen sie den jeweils eingestellten Wert ohne Zeitverzug im zugehörigen Label an. Praktisch!
Der Button "Shoot" löst einen Schuss aus, und zwar mit den in den Reglern vorgegebenen Werten für Geschwindigkeit und Abschusswinkel des Balles. Die zugehörige Callback-Funktion ab Zeile 80 in Listing 3 liest erst die eingestellten Reglerwerte aus und ruft dann die Funktion animate() aus Listing 4 auf, die den Ballverlauf ins Spielfeld einzeichnet und einen wahren Wert zurückgibt, falls der Ball im Tor gelandet ist. Ist er verhungert oder hat der Torhüter ihn abgefangen, kommt ein falscher Wert zurück. Im Erfolgsfall erhöht sich der Torzähler count um Eins, und itemsXPos() knobelt eine neue Spielsituation aus. Die Fyne-Funktion Move() stellt die Widgets für Tor und Torwart (Englisch "Goal" bzw. "Goalie") auf die neuen Positionen ein und auch die zugehörigen Texttafeln wandern mit. Wie bei allen Änderungen an UI-Widgets passt erst ein nachfolgender Aufruf von Refresh() das Spielfeld entsprechend an.
Wie üblich in graphischen Anwendungen definiert das Hauptprogramm alle möglichen Reaktionen auf User-Eingaben zuerst und tritt dann in Zeile 108 mit ShowAndRun() in die endlos währende Haupteventschleife ein. Klickt der User den "Quit"-Button, läutet os.Exit() das Programmende ein und die UI fällt sang- und klanglos in sich zusammen.
Was nun auf der Spielfläche passiert, wenn der User den "Shoot"-Button anklickt, definiert Listing 4 mit der Funktion animate(). Mit der Anfangsgeschwindigkeit des Balls (velo) sowie dem Abschusswinkel angle in Grad zeichnet sie die Flugbahn in den Spiel-Container ein und wertet eventuelle Kollisionen des Balles mit dem Torwart oder dem Tor anhand derer aktueller Positionen aus.
01 package main
02
03 import (
04 "math"
05 "time"
06
07 "fyne.io/fyne/v2"
08 "fyne.io/fyne/v2/canvas"
09 )
10
11 func animate(velo float64, angle float64, ui UI) bool {
12 nap := 10 // ms
13 now := 0
14
15 angle = math.Pi * angle / 180 // radient
16 rollout := 50
17
18 for {
19 pos := ui.ball.Position()
20 x, y := chipShot(velo, angle, float64(now)/100)
21 if y == 0 {
22 rollout--
23 if rollout < 0 {
24 break
25 }
26 }
27
28 goalYOff := float32(30)
29 pos.X = float32(x) * 20
30 pos.Y = gameHeight - goalYOff - float32(y)*100
31
32 ui.ball.Move(pos)
33 canvas.Refresh(ui.ball)
34
35 // goal?
36 if pos.X >= ui.goal.Position().X &&
37 pos.X <= ui.goal.Position().X+ui.goal.Size().Width &&
38 pos.Y > gameHeight-goalYOff-ui.goal.Size().Height {
39 go blink(ui.goalText)
40 return true
41 }
42
43 // goalie?
44 if pos.X >= ui.goalie.Position().X &&
45 pos.X <= ui.goalie.Position().X+ui.goalie.Size().Width &&
46 pos.Y > gameHeight-goalYOff-ui.goalie.Size().Height {
47 go blink(ui.goalieText)
48 break
49 }
50
51 time.Sleep(time.Duration(nap) * time.Millisecond)
52 now = now + 1
53 }
54 return false
55 }
56
57 func blink(tw fyne.CanvasObject) {
58 for i := 0; i < 3; i++ {
59 tw.Show()
60 canvas.Refresh(tw)
61 time.Sleep(250 * time.Millisecond)
62 tw.Hide()
63 canvas.Refresh(tw)
64 time.Sleep(250 * time.Millisecond)
65 }
66 }
67
68 func placeTextHover(tw, w fyne.CanvasObject) {
69 textPos := w.Position()
70 textPos.Y = textPos.Y - textHover
71 tw.Move(textPos)
72 tw.Hide()
73 }
Dazu wandelt Zeile 15 den vom Regler kommenden Gradwert des Abschusswinkels ins Radiant-Format um. Die Endlos-Schleife ab Zeile 18 in Listing 4 arbeitet die Animation des Videospiels ab, indem sie einzelne aufeinanderfolgende Frames im zeitlichen Abstand von 10 Millisekunden berechnet. Dabei bestimmt der Aufruf der Funktion chipShot() (aus Listing 1) in Zeile 20 die zum aktuellen Frame am Zeitwert now gehörende Ballposition auf der Parabelbahn als X- und Y-Werte. Dies passiert 100 Mal pro Sekunde, damit die Anzeige nicht ruckelt. Die Zeilen 32-33 frischen bei jedem durchlaufenen Frame die Ball-Position auf, mehr bewegt sich nichts auf dem Spielfeld während der Flugphase.
Beendet der Ball seine Flugbahn, weil er wieder zur Erde zurückgekehrt ist, liefert die Physik-Funktion chipShot() einen Y-Wert von Null und als vereinfachte Näherung lässt die Variable rollout den Ball noch 20 Frames am Boden weiterrollen. In Wirklichkeit spränge der Ball zurück in die Luft und würde erst nach ein paar solchen Hopsern entsprechend der Bodenreibung ausrollen, aber das vernachlässigt das Programm, damit die Formel einfach bleibt.
Etwaige Kollisionen des Balls mit dem Tor oder dem Torwart berechnen die if-Konstrukte der Zeilen 36 und 44. Sie prüfen, ob sich die aktuelle Ballposition irgendwo innerhalb der geometrischen Koordinaten von Tor oder Torwart befindet, und melden ein Tor mit blinkendem Text, falls der Ball im Tor ist, oder schalten die Torwartmeldung, falls der Keeper sich den Ball geschnappt hat.
Bevor die for-Schleife in die nächste Runde geht, schläft Zeile 51 zehn Millisekunden, zählt das Nickerchen zur aktuellen Zeit in now hinzu und weiter geht's zum nächsten Frame. Die blinkende Anzeige eines Tors oder Torwarterfolgs erledigt die Funktion blink() ab Zeile 57. Sie wird jeweils mit go aus animate() aufgerufen, damit sie nicht den laufenden Betrieb aufhält, sondern im Hintergrund läuft, während das Hauptprogramm sich weiter um User-Eingaben kümmern kann.
Das Binary chipshot entsteht, wie unter Go üblich, mit der folgenden Sequenz, denn der Compiler löst zunächst die im Code verwendeten Pakete und deren Abhängigkeiten auf:
go mod init chipshot
go mod tidy
go build chipshot.go animate.go physics.go
./chipshotUnd noch einige Tipps an die aufstrebende Fußballjugend: Steht der Torwart weit vor dem Tor und schon fast vor dem Angreifer, führt nur ein steil hoch geschossener Ball (etwa 60°) am Torwart vorbei, doch der Schuss braucht Schmackes, damit der Ball auf seiner steilen Bahn auch erst kurz vor dem Tor wieder herunterkommt und hoffentlich hineinkullert. In Spielsituationen, in denen der Torwart nur mäßig weit herausgelaufen ist, tut's oft ein Schuss mit 45° Anstellwinkel und mäßiger Geschwindigkeit. Und wie immer hilft: Trainieren, trainieren, trainieren!
Listings zu diesem Artikel: http://www.linux-magazin.de/static/listings/magazin/2021/11/snapshot/
Beispiel-Code zum Fyne-Buch, https://github.com/PacktPublishing/Building-Cross-Platform-GUI-Applications-with-Fyne
Michael Schilli, "Runter kommen sie alle", Michael Schilli, Linux-Magazin 10/2007, https://www.linux-magazin.de/ausgaben/2007/10/runter-kommen-sie-alle/
"Classic Game Design", Franz Lanzinger, 2019, https://www.amazon.com/dp/B07S3ZW1Z8
100.000 Viertel-Dollar-Münzen in einem Spielautomaten in Santa Cruz, "Digital Press Issue #49", https://www.digitpress.com/library/newsletters/digitalpress/dp52.pdf#page=12
"Chip" oder "Lob", ein Pass über den Gegenspieler im Fußball (auch "Bogenlampe"), https://de.wikipedia.org/wiki/Bogenlampe_(Sport)
Schiefer Wurf (Wurfparabel), Wikipedia, https://de.wikipedia.org/wiki/Wurfparabel
Vintage-Videospiel "Crystal Castles", https://en.wikipedia.org/wiki/Crystal_Castles_(video_game)
Hey! The above document had some coding errors, which are explained below:
Unknown directive: =desc